
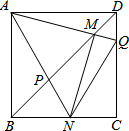
 如图,边长为1的正方形ABCD,Q是CD上一动点(不与点C、D重合),连接AQ交BD于点M,过M作MN⊥AQ交BC于N点,连接AN交BD于点P,在点Q运动过程中有下列结论:①AM=MN;②BM•DP=1;③存在点Q,使得BN+DQ=1;④$\sqrt{2}$BM-BN=1.其中一定成立的是①②④.
如图,边长为1的正方形ABCD,Q是CD上一动点(不与点C、D重合),连接AQ交BD于点M,过M作MN⊥AQ交BC于N点,连接AN交BD于点P,在点Q运动过程中有下列结论:①AM=MN;②BM•DP=1;③存在点Q,使得BN+DQ=1;④$\sqrt{2}$BM-BN=1.其中一定成立的是①②④. 分析 ①作AU⊥NQ于U,连接AN,AC,由∠AMN=∠ABC=90°,得到A,B,N,M四点共圆,推出∠NAM=∠DBC=45°,∠ANM=∠ABD=45°,得到等腰直角三角形AM=MN;
②由∠AMB=45°+∠DAM,∠DAP=45十∠DAM,得到∠DAP=∠BMA,根据相似三角形的性质得到BM:AD=AB:PD,于是得到BM.DP=AB.AD=1.
③由∠BAN+∠QAD=∠NAQ=45°在∠NAM内作AU=AB=AD,且使∠BAN=∠NAU,∠DAQ=∠QAU,构造全等三角形△ABN≌△UAN,△DAQ≌△UAQ,推出∠UAN=∠UAQ,BN=NU,DQ=UQ,点U在NQ上,有BN+DQ=QU+UN=NQ≠1;
④作MS⊥AB,垂足为S,作MW⊥BC,垂足为W,点M是对角线BD上的点,得到四边形SMWB是正方形,有MS=MW=BS=BW,得到△AMS≌△NMW证得AS=NW,推出AB+BN=SB+BW=2BW,由BW:BM=1:$\sqrt{2}$,得到$\frac{AN+BN}{BM}=\frac{2}{\sqrt{2}}=\sqrt{2}$,推出$\sqrt{2}$BM-BN=1.
解答 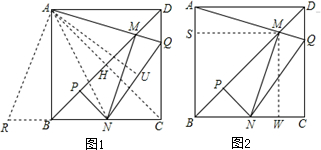 证明:①如图1,作AU⊥NQ于U,连接AN,AC,
证明:①如图1,作AU⊥NQ于U,连接AN,AC,
∵∠AMN=∠ABC=90°,
∴A,B,N,M四点共圆,
∴∠NAM=∠DBC=45°,∠ANM=∠ABD=45°,
∴∠ANM=∠NAM=45°,
∴AM=MN;
∴①正确;
②∠AMB=45°+∠DAM,
∵∠DAP=45十∠DAM,
∴∠DAP=∠BMA,
又∵∠ABM=∠PDA=45°,
∴△ABM∽△PDA,
∴BM:AD=AB:PD,
∴BM.DP=AB.AD=1
故②正确;
③∵∠BAN+∠QAD=∠NAQ=45°,
∴在∠NAM内作AU=AB=AD,且使∠BAN=∠NAU,∠DAQ=∠QAU,
∴△ABN≌△UAN,△DAQ≌△UAQ,有∠UAN=∠UAQ,BN=NU,DQ=UQ,
∴点U在NQ上,有BN+DQ=QU+UN=NQ≠1;
∴③错误;
④如图2,作MS⊥AB,垂足为S,作MW⊥BC,垂足为W,点M是对角线BD上的点,
∴四边形SMWB是正方形,有MS=MW=BS=BW,
∴△AMS≌△NMW,
∴AS=NW,
∴AB+BN=SB+BW=2BW,
∵BW=$\frac{\sqrt{2}}{2}$BM,
∴AB+BN=2BW=2($\frac{\sqrt{2}}{2}$BM)=$\sqrt{2}$BM,
∴$\sqrt{2}$BM-BN=1,
∴④正确.
故答案为:①②④.
点评 本题考查了正方形的性质,四点共圆的判定,圆周角定理,等腰直角三角形的性质,全等三角形的判定和性质等知识,正确作出辅助线并运用有关知识理清图形中线段间的关系是解答本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{2}{x}$ | B. | y=-$\frac{4}{x}$ | C. | y=3x+2 | D. | y=x2-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某公园管理人员在巡视公园时,发现有一条圆柱形的输水管道破裂,通知维修人员到场检测,维修员画出水平放置的破裂管道有水部分的截面图(如图).
某公园管理人员在巡视公园时,发现有一条圆柱形的输水管道破裂,通知维修人员到场检测,维修员画出水平放置的破裂管道有水部分的截面图(如图).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
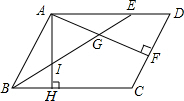 在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )
在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 6 | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2cm | B. | 2$\sqrt{2}$cm | C. | 2$\sqrt{3}$cm | D. | 4cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com