
分析 (1)①-②消去x与z求出y的值,然后将y的值代入②和③,然后解关于x与z的二元一次方程组即可得到原方程组的解;
(2)①×3+②消去y,得到11x+z=23④,然后将②④联立方程组,解此方程组得到x与z的值,然后将x的值代入①求出y的值,即可得到原方程组的解.
解答 解:(1)$\left\{\begin{array}{l}{x+y+z=2①}\\{x-2y+z=-1②}\\{x+2y+3z═-1③}\end{array}\right.$,
①-②得:y=1,
将y=1,代入②和③得:x+z=1④,x+3z=-3⑤,
然后将④和⑤联立方程组得:$\left\{\begin{array}{l}{x+z=1④}\\{x+3z=-3⑤}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=3}\\{z=-2}\end{array}\right.$,
所以原方程组的解为:$\left\{\begin{array}{l}{x=3}\\{y=1}\\{z=-2}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x-y=7①}\\{5x+3y+z=2②}\\{3x-4z=2③}\end{array}\right.$,
①×3+②得:11x+z=23④,
将③,④联立方程组得:得:$\left\{\begin{array}{l}{3x-4z=2③}\\{11x+z=23④}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2}\\{z=1}\end{array}\right.$,
将x=2代入①得:y=-3,
所以原方程组的解为:$\left\{\begin{array}{l}{x=2}\\{y=-3}\\{z=1}\end{array}\right.$.
点评 本题考查了三元一次方程组,利用加减消元法或代入消元法把三元一次方程组转化为二元一次方程组进行求解,是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1cm<AB<4cm | B. | 3cm<AB<6cm | C. | 4cm<AB<8cm | D. | 5cm<AB<10cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 保证“神舟九号”载人飞船成功发射,对重要零部件的检查 | |
| B. | 了解人们对环境保护的意识 | |
| C. | 了解一批灯泡的使用寿命 | |
| D. | 了解央视2013年“春节联欢晚会”栏目的收视率 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
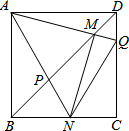 如图,边长为1的正方形ABCD,Q是CD上一动点(不与点C、D重合),连接AQ交BD于点M,过M作MN⊥AQ交BC于N点,连接AN交BD于点P,在点Q运动过程中有下列结论:①AM=MN;②BM•DP=1;③存在点Q,使得BN+DQ=1;④$\sqrt{2}$BM-BN=1.其中一定成立的是①②④.
如图,边长为1的正方形ABCD,Q是CD上一动点(不与点C、D重合),连接AQ交BD于点M,过M作MN⊥AQ交BC于N点,连接AN交BD于点P,在点Q运动过程中有下列结论:①AM=MN;②BM•DP=1;③存在点Q,使得BN+DQ=1;④$\sqrt{2}$BM-BN=1.其中一定成立的是①②④.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com