
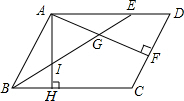
 在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )
在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 6 | D. | 3$\sqrt{3}$ |
分析 由平行四边形的性质得到对边平行,得出内错角相等,因为BE平分∠ABC,得到∠1=∠3,证得∠2=∠3,得到AB=AE,由△ABC∽△ADF,得到∠4=∠5,通过三角形全等推出BI=EG,由BI=IG,得到GE=IG,应用直角三角形的性质得出IE的长度,根据勾股定理解出结果.
解答 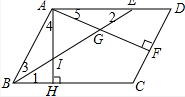 解:在?ABCD中,
解:在?ABCD中,
∵AD∥BC,
∴∠1=∠2
∵∠1=∠3,
∴∠2=∠3,
∴AB=AE,
∵AF⊥CD,AH⊥BC,
∴∠AHB=∠AFD=90°,
在平行四边形ABCD中,∠ABH=∠ADF,
∴△ABH∽△ADF,
∴∠4=∠5
在△ABI与△AEG中,$\left\{\begin{array}{l}{∠4=∠5}\\{∠3=∠2}\\{AB=AE}\end{array}\right.$,
∴△ABI≌△AEG,
∴BI=EG,∵BI=IG,
∴GE=IG,
∵AD∥BC,
∴∠DAH=∠AHB=90°,
∴IE=2AG=2AI=6,
∴AE=$\sqrt{{IE}^{2}{-AI}^{2}}$=3$\sqrt{3}$.
故选D.
点评 此题考查了平行四边形的性质、勾股定理,相似三角形的判定和性质,全等三角形的判定与性质,直角三角形的性质,解题的关键是证出△AIE是直角三角形并应用其性质.


科目:初中数学 来源: 题型:选择题
| A. | 1cm<AB<4cm | B. | 3cm<AB<6cm | C. | 4cm<AB<8cm | D. | 5cm<AB<10cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
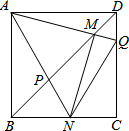 如图,边长为1的正方形ABCD,Q是CD上一动点(不与点C、D重合),连接AQ交BD于点M,过M作MN⊥AQ交BC于N点,连接AN交BD于点P,在点Q运动过程中有下列结论:①AM=MN;②BM•DP=1;③存在点Q,使得BN+DQ=1;④$\sqrt{2}$BM-BN=1.其中一定成立的是①②④.
如图,边长为1的正方形ABCD,Q是CD上一动点(不与点C、D重合),连接AQ交BD于点M,过M作MN⊥AQ交BC于N点,连接AN交BD于点P,在点Q运动过程中有下列结论:①AM=MN;②BM•DP=1;③存在点Q,使得BN+DQ=1;④$\sqrt{2}$BM-BN=1.其中一定成立的是①②④.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
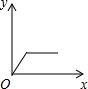 如图是反应两个变量关系的图,下列的四个情境比较适合该图的是( )
如图是反应两个变量关系的图,下列的四个情境比较适合该图的是( )| A. | 一辆汽车从起动到匀速行驶,速度与时间的关系 | |
| B. | 一杯热水放在桌子上,它的水温与时间的关系 | |
| C. | 一架飞机从起飞到降落的速度与时间的关系 | |
| D. | 一个踢出的足球的速度与时间的关系 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com