
分析 (1)先算乘法,再合并同类项,最后代入求出即可;
(2)先展开,合并后根据平方差公式分解即可.
解答 解:(1)(2x+3y)2-(2x+y)(2x-y)
=4x2+12xy+9y2-4x2+y2
=12xy+10y2,
当x=$\frac{1}{3}$,y=$-\frac{1}{2}$时,原式=12×$\frac{1}{3}$×(-$\frac{1}{2}$)+10×(-$\frac{1}{2}$)2=$\frac{1}{2}$;
(2)(p2-16)(p2+1)+15p2
=p4-15p2-16+15p2
=p4-16
=(p2+4)(p2-4)
=(p2+4)(p+2)(p-2).
点评 本题考查了整式的混合运算和求值,分解因式的应用,能正确运用整式的运算法则进行化简和能选择适当的方法分解因式是解此题的关键,难度适中.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | y=$\frac{2}{x}$ | B. | y=-$\frac{4}{x}$ | C. | y=3x+2 | D. | y=x2-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
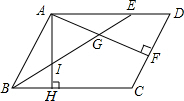 在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )
在?ABCD中,BE平分∠ABC交AD于点E,AF⊥CD于点F,交BE于点G,AH⊥BC于点H,交BE于点I.若BI=IG,且AI=3,则AE的长为( )| A. | 3 | B. | 2$\sqrt{3}$ | C. | 6 | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
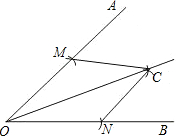 如图,已知∠AOB,按照以下步骤画图:
如图,已知∠AOB,按照以下步骤画图:| A. | 边边边 | B. | 边角边 | C. | 角边角 | D. | 角角边 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
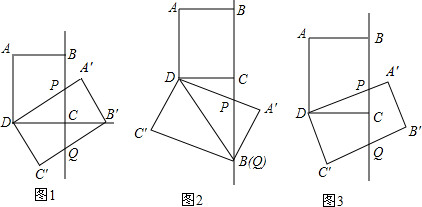
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2cm | B. | 2$\sqrt{2}$cm | C. | 2$\sqrt{3}$cm | D. | 4cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com