
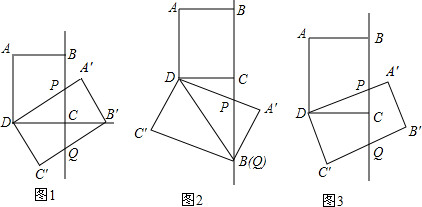
���� ��1���ٸ������������ε����ʵó��ߵı�ֵ���ɣ�
����ȫ�������ε��ж������ʵó��ߵĹ�ϵ���ٸ��ݹ��ɶ����ó����̽�ɣ�
��2�����ɾ��ε����ʵó��߶���ȣ�������ȫ�������ν����жϣ�����������֤�����ɣ�
�ڸ���ȫ���������ж������ʵó��߶ι�ϵ�������ù��ɶ����ó����̽�ɣ�
��3���ּ���������з����ó��Ե�D��B�䣬P��QΪ������ı����ܷ��Ϊƽ���ı��Σ������ó�CP��ֵ��
��� 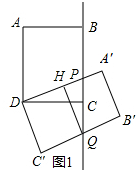 �⣺��1���١߽�����ABCD�Ƶ�D��˳ʱ�뷽����ת���õ�����A��B��C��D�䣬AB=6��BC=8��
�⣺��1���١߽�����ABCD�Ƶ�D��˳ʱ�뷽����ת���õ�����A��B��C��D�䣬AB=6��BC=8��
���CDP�ס�A'DB'��
��CP=$\frac{9}{2}$��
ͬ��CQ=3��
��BP=$\frac{7}{2}$��PQ=$\frac{15}{2}$��
��$\frac{BP}{PQ}=\frac{7}{15}$��
���ڡ�DCP�͡�A'DB'�У�
$\left\{\begin{array}{l}{��DPC=��B'PA'}\\{��DCP=��A'=90��}\\{DC=B'A'}\end{array}\right.$��
���DCP�ա�A'DB'��AAS����
��CP=A'P��
��DP=x��
��DP=B'P��
��B'P=x���ɵã�8-x��2+62=x2��
��ã�x=$\frac{25}{4}$��
��2������ͼ1������Q��QH��DA'��H��
���QHD=��HDC'=��C'=90�㣬
���ı���QHDC'Ϊ���Σ�
��QH=DC'=DC��
�ڡ�DCP�͡�QHP�У�
$\left\{\begin{array}{l}{��QHP=��DCP=90��}\\{��QPH=��DPC}\\{QH=DC}\end{array}\right.$��
���DCP�ա�QHP��AAS����
��DP=PQ��
�ڣ�����P�ڵ�B�Ϸ�ʱ����ͼ2��
ͬ��2���ٿɵá��DCP�ա�QHP��AAS����
��DP=PQ��
��BP=$\frac{1}{2}$BQʱ��BQ=2BP=2x��
��DP=PQ=BP+BQ=3x��
��Rt��PCD����8+x��2+62=��3x��2��
��ã�${x}_{1}=1+\frac{3}{2}\sqrt{6}��{x}_{2}=1-\frac{3}{2}\sqrt{6}$��С��0����ȥ����
��PC=BC+BP=$9+\frac{3}{2}\sqrt{6}$��
����P���߶�BC��ʱ����DP=PQ=BP=x��PC=8-x��
��Rt��PCD����8-x��2+62=x2��
���x=$\frac{25}{4}$��
��PC=BC-PB=8-$\frac{25}{4}$=$\frac{7}{4}$��
�����ABCD��ת����0�㣼����90��ʱ�������У�
��BP=$\frac{1}{2}$BQʱ��CP�ij���$9+\frac{3}{2}\sqrt{6}$��$\frac{7}{4}$��
��3�������DA��B��C��ĶԽ�����ֱ��BC�Ľ���ΪS��
�ٵ�B����ֱ��BC���Ҳ�ʱ����ȻDP��B��Q��
������DS��DC��$\frac{1}{2}D{B}^{'}$=5����PQ��DB�䲻����ƽ�֣�
����D��B�䣬P��QΪ������ı��β��ܹ���ƽ���ı��Σ�
�ڵ�B����ֱ��BC��ʱ��B�䣬P��Q������һ��ֱ���ϣ�
����D��B�䣬P��QΪ������ı��β��ܹ���ƽ���ı��Σ�
�۵�B�������߶�AD���ӳ�����ʱ��DP��B��Q��
��DB���PQ�������ı���DB��PQ��ƽ���ı��Σ�
��ʱCP=D��A=8��
�ܵ�B����ֱ��BC��ֱ��AD��������ʱ����ȻDP��B��Q��
��DB����PQ��ƽ�У�����D��B�䣬P��QΪ������ı��β��ܹ���ƽ���ı��Σ�
������������B�������߶�AD���ӳ�����ʱ���ı���DB��PQ��ƽ���ı��Σ���ʱCP=8��
���� ���⿼���˾��ε����ʣ���ת�����ʣ�ȫ�������ε��ж������ʣ����ɶ�����Ӧ�õȣ��ҳ����������εĸߵĹ�ϵ�DZ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
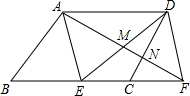 ��?ABCD�У���E��BC���ϣ���F��BC�ߵ��ӳ����ϣ���BE=CF��
��?ABCD�У���E��BC���ϣ���F��BC�ߵ��ӳ����ϣ���BE=CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����Ϊԭ����3�� | B�� | ��СΪԭ����$\frac{1}{3}$ | C�� | ���� | D�� | ��СΪԭ����$\frac{1}{9}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com