
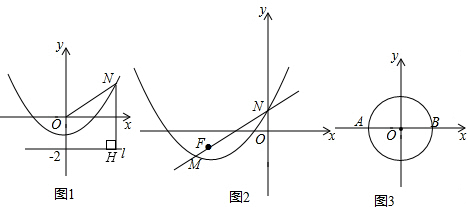
���� ��1���ٸ��ݹ��ɶ������ɵ�ON�ij������ݵ㵽ֱ�ߵľ��룬�ɵÿɵ�NH�ij���
�ڸ���ͼ���ϵĵ����㺯������ʽ���ɵõ�����꣬���ݹ��ɶ������ɵ�NO�ij������ݵ㵽ֱ�ߵľ��룬�ɵ�NH�ij���
��2���ٸ��������ߵġ��ߡ��Ķ��弴�ɵõ�������y2�ġ��ߡ�l��
�������MQ��NH�ij������뼴����⣻
��2��������������ٵ������㡱Ϊ${F_1}��{\frac{1}{2}��-\frac{{\sqrt{3}}}{2}}��$������Ϊ$��{\frac{1}{2}��-\frac{{\sqrt{3}}}{4}}��$��C��2��0��ʱ���ڵ������㡱Ϊ${F_2}��{\frac{1}{2}��\frac{{\sqrt{3}}}{2}}��$������Ϊ$��{-\frac{1}{2}��\frac{{\sqrt{3}}}{4}}��$��C��-2��0��ʱ���������ۿɵ���FΪ�����㡱��x��Ϊ���ߡ���������${y_3}=a{x^2}+bx+c$�ı���ʽ��
��� �⣺��1���ٵ�m=0ʱ��N��0��-1����ON=1��NH=-1-��-2��=1��
��m=4ʱ��y=3��N��4��3����ON=$\sqrt{{4}^{2}+{3}^{2}}$=5��NH=3-��-2��=3+2=5��
�ʴ�Ϊ��1��5�� ��2�����룺NO=NH��
��2�����룺NO=NH��
֤������ͼ1��NH��x�����Q��
��N��y=$\frac{1}{4}$x2-1�ϣ�
����N��m��$\frac{1}{4}$m2-1����NQ=|$\frac{1}{4}$m2-1|��OQ=|m|��
�ߡ�ONQ��ֱ�������Σ�
��ON=$\sqrt{N{Q}^{2}+O{Q}^{2}}$=$\sqrt{��\frac{1}{4}{m}^{2}-1��^{2}+{m}^{2}}$=$\sqrt{��\frac{1}{4}{m}^{2}+1��^{2}}$=$\frac{1}{4}$m2+1��
NH=yN-��-2��=��$\frac{1}{4}$m2-1��-��-2��=$\frac{1}{4}$m2+1
ON=NH��
�ʴ�Ϊ��=��
��Ӧ�á���1����������y2�ġ��ߡ�l��y=-3��
�ʴ�Ϊ��y=-3��
��$\frac{1}{MQ}+\frac{1}{NH}$=$\frac{4}{5}$+$\frac{1}{5}$=1��
�ʴ�Ϊ��1��
��2����ͼ3����ֱ��$y=\frac{{\sqrt{3}}}{3}x+n$��x���ཻ�ڵ�C��
�������ֱ֪��CF�С�O��F������OF��
���OFC=90��
���COF=60��
�֡�OF=1��
��OC=2��
��C����2��0����
�ࡰ���㡱${F_1}��{\frac{1}{2}��-\frac{{\sqrt{3}}}{2}}��$��${F_2}��{-\frac{1}{2}��\frac{{\sqrt{3}}}{2}}��$��
��������y3�Ķ���Ϊ$��{\frac{1}{2}��-\frac{{\sqrt{3}}}{4}}����{-\frac{1}{2}��\frac{{\sqrt{3}}}{4}}��$��
�ٵ������㡱Ϊ${F_1}��{\frac{1}{2}��-\frac{{\sqrt{3}}}{2}}��$������Ϊ$��{\frac{1}{2}��-\frac{{\sqrt{3}}}{4}}��$��C��2��0��ʱ��
��ֱ��CF1��$y=\frac{{\sqrt{3}}}{3}x-\frac{2}{3}\sqrt{3}$��
����A��AM��x�ᣬ��ֱ��CF1�ڵ�M��
��MA=MF1��
��$M��{-1��-\sqrt{3}}��$��������y3�ϣ�
��������${y_3}=a{��{x-\frac{1}{2}}��^2}-\frac{{\sqrt{3}}}{4}$����M������������ã�$a=-\frac{{\sqrt{3}}}{3}$��
��${y_3}=-\frac{{\sqrt{3}}}{3}{��{x-\frac{1}{2}}��^2}-\frac{{\sqrt{3}}}{4}=-\frac{{\sqrt{3}}}{3}{x^2}+\frac{{\sqrt{3}}}{3}x-\frac{{\sqrt{3}}}{3}$��
�ڵ������㡱Ϊ${F_2}��{\frac{1}{2}��\frac{{\sqrt{3}}}{2}}��$������Ϊ$��{-\frac{1}{2}��\frac{{\sqrt{3}}}{4}}��$��C��-2��0��ʱ��
�����ĶԳ��Կɵã�y3=$\frac{\sqrt{3}}{3}$��x+$\frac{1}{2}$��2+$\frac{\sqrt{3}}{4}$=$\frac{\sqrt{3}}{3}$x2+$\frac{\sqrt{3}}{3}$x+$\frac{\sqrt{3}}{3}$��
����������������${y_3}=-\frac{{\sqrt{3}}}{3}{x^2}+\frac{{\sqrt{3}}}{3}x-\frac{{\sqrt{3}}}{3}$��y3=$\frac{\sqrt{3}}{3}$x2+$\frac{\sqrt{3}}{3}$x+$\frac{\sqrt{3}}{3}$��
���� ���⿼���˶��κ����ۺ��⣬�����˹��ɶ������㵽ֱ�ߵľ��룬�߶��е�����ʣ��߶εĺͲ�����ߵġ����㡱�������ߵġ��ߡ��Ķ��壬����˼���Ӧ�ã����õ�֪ʶ��϶࣬��Ŀ�����Ѷȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 11 | B�� | 13 | C�� | 11��13 | D�� | 12��13 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ƽ���ı���ABCD�ĶԽ��߽��ڵ�O����AB=7����OCD���ܳ�Ϊ23����ƽ���ı���ABCD�������Խ��ߵĺ��ǣ�������
��ͼ��ƽ���ı���ABCD�ĶԽ��߽��ڵ�O����AB=7����OCD���ܳ�Ϊ23����ƽ���ı���ABCD�������Խ��ߵĺ��ǣ�������| A�� | 32 | B�� | 28 | C�� | 16 | D�� | 46 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com