
分析 本题的关键语“每件降价1元时,平均每天可多卖出2件”,设每件应降价x元,用x来表示出商场所要求的每件盈利的数额量,然后根据盈利1200元来列出方程;
解答 解:设每件应降价x 元,由题意可列方程为(40-x )(30+2x )=1200,
解得x1=0,x2=25,
当x=0 时,能卖出30 件;
当x=25 时,能卖出80件,
根据题意,x=25 时能卖出80 件,符合题意,不降价也能盈利1200元,符合题意,
因为要减少库存,所以应降价25 元,
答:每件衬衫应降价25元;
点评 本题主要考查一元二次方程的应用,关键在于理解清楚题意找出等量关系列出方程求解,此题问题更是中考的热点考题之一,难度不大.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
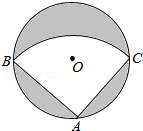 如图,有一直径是$\sqrt{2}$米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )
如图,有一直径是$\sqrt{2}$米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,用该扇形铁皮围成一个圆锥,则所得圆锥的底面圆的半径为( )| A. | $\frac{{\sqrt{2}}}{2}$米 | B. | $\frac{{\sqrt{2}}}{4}$米 | C. | $\frac{1}{2}$米 | D. | $\frac{1}{4}$米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com