
 ij��������Ա��Ѳ�ӹ�ʱ��������һ��Բ���ε���ˮ�ܵ����ѣ�֪ͨά����Ա������⣬ά��Ա����ˮƽ���õ����ѹܵ���ˮ���ֵĽ���ͼ����ͼ����
ij��������Ա��Ѳ�ӹ�ʱ��������һ��Բ���ε���ˮ�ܵ����ѣ�֪ͨά����Ա������⣬ά��Ա����ˮƽ���õ����ѹܵ���ˮ���ֵĽ���ͼ����ͼ�������� ��1�����ݳ߹���ͼ�IJ���ͷ�������ͼ���ɣ�
��2���ȹ�Բ��O���뾶CO��AB����AB�ڵ�D��뾶Ϊr���ó�BD��OD�ij�����Rt��AOD�У����ݹ��ɶ���������Բ�ν���İ뾶����ֱ�����Ǻ�����á�DOB=60�㣬Ȼ�����S=S����OACB���-S��OAB�����ü��ɣ�
��� �⣺��1����ͼ��
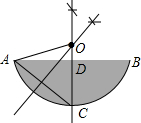
��2������O��OC��AB��D������AB��C����CD=6cm��
��OC��AB��
��BD=$AD=\frac{1}{2}AB$��
��$AB=12\sqrt{3}$cm��
��BD=$AD=6\sqrt{3}$cm��
�߰뾶Ϊrcm����OD=��r-6��cm��
��Rt��BOD �У��ɹ��ɶ����ã�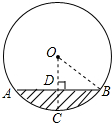
BD2+OD2=BO2��
��${��6\sqrt{3}��^2}+{��r-6��^2}={r^2}$��
���r=12��
�����Բ�ν���İ뾶Ϊ12cm��
�֡��軡��AB����Բ�Ľ�Ϊ�ȣ���$��DOB=\frac{1}{2}��$��
��Rt��BOD��BD=$6\sqrt{3}$��OB=12��
��$sin��DOB=\frac{BD}{OB}=\frac{{\sqrt{3}}}{2}$���ҡ�DOBΪRt��BOD��һ���ڽǣ�
���$��DOB=\frac{1}{2}��$=60��
���=120��
��S=S����OACB���-S��OAB���=$\frac{120}{360}•��•{12^2}-\frac{1}{2}��12\sqrt{3}��6$
=$48��-36\sqrt{3}$��cm2����
���� ���⿼���˴����������ɶ����Լ���ֱ�������Σ��ؼ��Ǹ������⻭��ͼ�Σ��ٸ��ݹ��ɶ������OD��BD�����ݽ�ֱ����������á�DOB=60�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
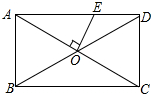 ��ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O������O��OE��AC��AD��E����AB=6��AD=8����sin��OEA��ֵ��
��ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O������O��OE��AC��AD��E����AB=6��AD=8����sin��OEA��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
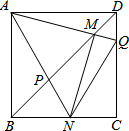 ��ͼ���߳�Ϊ1��������ABCD��Q��CD��һ���㣨�����C��D�غϣ�������AQ��BD�ڵ�M����M��MN��AQ��BC��N�㣬����AN��BD�ڵ�P���ڵ�Q�˶������������н��ۣ���AM=MN����BM•DP=1���۴��ڵ�Q��ʹ��BN+DQ=1����$\sqrt{2}$BM-BN=1������һ���������Ǣ٢ڢܣ�
��ͼ���߳�Ϊ1��������ABCD��Q��CD��һ���㣨�����C��D�غϣ�������AQ��BD�ڵ�M����M��MN��AQ��BC��N�㣬����AN��BD�ڵ�P���ڵ�Q�˶������������н��ۣ���AM=MN����BM•DP=1���۴��ڵ�Q��ʹ��BN+DQ=1����$\sqrt{2}$BM-BN=1������һ���������Ǣ٢ڢܣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��2��3 | B�� | 2��3��4 | C�� | 3��4��5 | D�� | 4��5��6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | l | C�� | 2 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com