
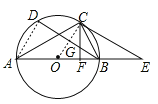
【题目】如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)求证:CG=BG;
(3)若∠DBA=30°,CG=4,求BE的长.

【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)连接OC,先证得![]() ,根据垂径定理得到OC⊥BD,根据CE∥BD推出OC⊥CE,即可得到结论;
,根据垂径定理得到OC⊥BD,根据CE∥BD推出OC⊥CE,即可得到结论;
(2)根据圆周角定理得出∠ACB=90°,然后根据同角的余角相等得出∠A=∠BCF,即可证得∠BCF=∠CBD,根据同角对等边即可证得结论;
(3)连接AD,根据圆周角定理得出∠ADB=90°,即可求得∠BAD=60°,根据圆周角定理得出∠DAC=∠BAC=30°,解直角三角形求得![]() =tan30°=
=tan30°=![]() ,然后根据三角形相似和等腰三角形的判定即可求得BE的值.
,然后根据三角形相似和等腰三角形的判定即可求得BE的值.
(1)证明:连接OC,∵∠A=∠CBD,∴ ![]() ,∴OC⊥BD,∵CE∥BD,∴OC⊥CE,∴CE是⊙O的切线;
,∴OC⊥BD,∵CE∥BD,∴OC⊥CE,∴CE是⊙O的切线;
(2)证明:∵AB为直径,∴∠ACB=90°,∵CF⊥AB,∴∠ACB=∠CFB=90°,∵∠ABC=∠CBF,∴∠A=∠BCF,∵∠A=∠CBD,∴∠BCF=∠CBD,∴CG=BG;
(3)解:连接AD,∵AB为直径,∴∠ADB=90°,∵∠DBA=30°,∴∠BAD=60°,∵![]() ,∴∠DAC=∠BAC=
,∴∠DAC=∠BAC=![]() ∠BAD=30°,∴
∠BAD=30°,∴![]() =tan30°=
=tan30°=![]() ,∵CE∥BD,∴∠E=∠DBA=30°,∴AC=CE,∴
,∵CE∥BD,∴∠E=∠DBA=30°,∴AC=CE,∴![]() =
=![]() ,∵∠A=∠BCF=∠CBD=30°,∴∠BCE=30°,∴BE=BC,∴△CGB∽△CBE,∴
,∵∠A=∠BCF=∠CBD=30°,∴∠BCE=30°,∴BE=BC,∴△CGB∽△CBE,∴![]() =
=![]() =
=![]() ,∵CG=4,∴BC=
,∵CG=4,∴BC=![]() ,∴BE=
,∴BE=![]() .
.


科目:初中数学 来源: 题型:
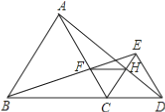
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,求证:
(1)△BCE≌△ACD;
(2)CF=CH;
(3)△FCH是等边三角形;
(4)FH∥BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y= ![]() (k>0,x>0)的图象上,点D的坐标为(
(k>0,x>0)的图象上,点D的坐标为( ![]() ,2).
,2).
(1)求k的值;
(2)若将菱形ABCD沿x轴正方向平移,当菱形的一个顶点恰好落在函数y= ![]() (k>0,x>0)的图象上时,求菱形ABCD平移的距离.
(k>0,x>0)的图象上时,求菱形ABCD平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
(1)①表中a的值为 , 中位数在第组;
②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场300名职工耕种51公顷土地,计划种植水稻,棉花和蔬菜,已知种植农作物每公顷所需的劳动力人数及投入的设备资金如下表:
农作物品种 | 每公顷需劳动力 | 每公顷需投入资金 |
水稻 | 4人 | 1万元 |
棉花 | 8人 | 1万元 |
蔬菜 | 5人 | 2万元 |
已知该农场计划在设备上投入67万元,应该怎样安排三种农作物的种植面积,才能使所有的职工都有工作,而且投入的资金正好够用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是不等边三角形, ![]() ,以
,以![]() ,
, ![]() 为两个顶点作位置不同的三角形,使所作△DEF与△ABC全等,这样的三角形最多可以画出( )
为两个顶点作位置不同的三角形,使所作△DEF与△ABC全等,这样的三角形最多可以画出( )

A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
【答案】B
【解析】试题解析:如图,可以作出这样的三角形4个.

故选B.
【题型】单选题
【结束】
9
【题目】作三角形用到的基本作图是:
(1)___________________________;(2)_______________________________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作三角形用到的基本作图是:
(1)___________________________;(2)_______________________________;
【答案】 作一个角等于已知角 作一条线段等于已知线段
【解析】试题解析:作三角形用到的基本作图是:(1). 作一个角等于已知角(2). 作一条线段等于已知线段
故答案为:(1). 作一个角等于已知角(2). 作一条线段等于已知线段.
【题型】填空题
【结束】
10
【题目】尺规作三角形的类型:
尺 规 作 图 | 类型 | 依据 |
已知两边及其夹角作三角形 | __________ | |
已知两角一边作三角形 | __________(或 | |
已知三边作三角形 | __________ |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线l1∥l2,且l3和l1,l2分别相交于A,B两点,l4和l1,l2分别交于C,D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3,
点P在线段AB上.
(1)若∠1=22°,∠2=33°,则∠3=________;
(2)试找出∠1,∠2,∠3之间的等量关系,并说明理由;
(3)应用(2)中的结论解答下列问题;
如图②,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数;
(4)如果点P在直线l3上且在A,B两点外侧运动时,其他条件不变,试探究∠1,∠2,∠3之间的关系(点P和A,B两点不重合),直接写出结论即可.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com