
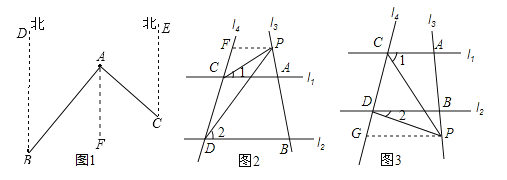
����Ŀ����ͼ�٣���ֱ֪��l1��l2����l3��l1��l2�ֱ��ཻ��A��B���㣬l4��l1��l2�ֱ���C��D���㣬��ACP����1����BDP����2����CPD����3��
��P���߶�AB����
(1)����1��22������2��33�������3��________��
(2)���ҳ���1����2����3֮��ĵ�����ϵ����˵�����ɣ�
(3)Ӧ��(2)�еĽ��۽������������
��ͼ������A��B����ƫ��40���ķ����ϣ���C���ı�ƫ��45���ķ����ϣ����BAC�Ķ�����
(4)�����P��ֱ��l3������A��B��������˶�ʱ�������������䣬��̽����1����2����3֮��Ĺ�ϵ(��P��A��B���㲻�غ�)��ֱ��д�����ۼ��ɣ�



���𰸡���1��55�㣻��2����1+��2=��3����3��85�㣻��4����CPD=|��1����2|.
�������������������1������ƽ���ߵ����ʺ��������ڽǺͶ������������
��2������ƽ���ߵ����ʺ��������ڽǺͶ������������
��3����A����AF��BD����AF��BD��CE������ƽ���ߵ����ʼ��������
��4���ֵ�P����A������뵱P����B���������������з������ۼ��ɣ�
���������������1����1+��2=��3��
��l1��l2�����1+��PCD+��PDC+��2=180��������PCD������3+��PCD+��PDC=180�������3=��1+��2=55�����ʴ�Ϊ��55����
��2����1+��2=��3������������
��l1��l2�����1+��PCD+��PDC+��2=180��������PCD������3+��PCD+��PDC=180�������1+��2=��3��
��3����A����AF��BD����AF��BD��CE������BAC=��DBA+��ACE=40��+45��=85����
��4����P����A�����ʱ����ͼ2����P��PF��l1����l4��F�����1=��FPC��
��l1��l4����PF��l2�����2=��FPD��
�ߡ�CPD=��FPD����FPC�����CPD=��2����1��
��P����B�����ʱ����ͼ3����P��PG��l2����l4��G�����2=��GPD��
��l1��l2����PG��l1�����1=��CPG��
�ߡ�CPD=��CPG����GPD�����CPD=��1����2��
������������CPD=|��1����2|��


 ʱ�����������ҵԭ���ܳ�����ϵ�д�
ʱ�����������ҵԭ���ܳ�����ϵ�д� ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ԡ�ABC�ı�ABΪֱ������O����C�ڡ�O�ϣ�BD�ǡ�O���ң���A=��CBD������C��CF��AB�ڵ�F����BD�ڵ�G����C��CE��BD��AB���ӳ����ڵ�E��
��1����֤��CE�ǡ�O�����ߣ�
��2����֤��CG=BG��
��3������DBA=30�㣬CG=4����BE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2018��ij����23 000�����б�ҵ���μ�����ѧ���ԣ�Ϊ�˽�23 000����������ѧ�ɼ������г�ȡ��200���������Ծ�����ͳ�Ʒ���������˵����ȷ���ǣ� ��
A.23 000������������B.ÿ�������ijɼ��Ǹ���
C.200�������������һ������D.����˵��������ȷ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪BF����O��ֱ����AΪ��O�ϣ�����B��F��һ�㣬��O������MA��FB���ӳ��߽��ڵ�M��PΪAM��һ�㣬PB���ӳ��߽���O�ڵ�C��DΪBC��һ����PA=PD��AD���ӳ��߽���O�ڵ�E��
��1����֤�� ![]() ��
��
��2����ED��EA�ij���һԪ���η���![]() ����������BE�ij���
����������BE�ij���
��3����MA=![]() ��sin��AMF=
��sin��AMF=![]() ����AB�ij���
����AB�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һ�κ���y=��2m-4��x+3n��
��1����m��nȡ��ֵʱ��y��x�����������
��2����m��nȡ��ֵʱ������ͼ��ԭ�㣿
��3����m��nȡ��ֵʱ������ͼ����y�ύ����x���Ϸ���
��4����ͼ��һ�����������ޣ���m��n��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����D=��C=90����E��DC���е㣬AEƽ�֡�DAB����DEA=28�������ABE�Ķ����ǣ� ��
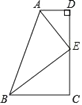
A. 62�� B. 31�� C. 28�� D. 25��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=BC����O��AB�ϣ�������A�ġ�O��BC�����ڵ�D����AB�ڵ�E��
��1����֤��ADƽ�֡�BAC��
��2����CD=1����ͼ����Ӱ���ֵ��������������У���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���ABC=��ACB����D��BC���ڵ�ֱ���ϣ���E������AC�ϣ���AD=AE������DE��
����ͼ�٣�����B=��C=35������BAD=80�������CDE�Ķ�����
����ͼ�ڣ�����ABC=��ACB=75������CDE=18�������BAD�Ķ�����
������D��ֱ��BC�ϣ������B��C�غϣ��˶�ʱ����̽����BAD���CDE��������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ı���ABCD�����Σ�����ABC=60����ABE�ǵȱ������Σ�MΪ�Խ���BD������B�㣩������һ�㣬��BM�Ƶ�B��ʱ����ת60���õ�BN������EN��AM��CM�������������������ȷ���ǣ�������
��������ABCD�ı߳�Ϊ1����AM+CM����Сֵ1��
�ڡ�AMB�ա�ENB��
��S�ı���AMBE=S�ı���ADCM��
������AN����AN��BE��
����AM+BM+CM����СֵΪ2![]() ʱ������ABCD�ı߳�Ϊ2��
ʱ������ABCD�ı߳�Ϊ2��

A. �٢ڢ� B. �ڢܢ� C. �٢ڢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com