
【题目】已知关于x的一次函数y=(2m-4)x+3n.
(1)当m,n取何值时,y随x的增大而增大?
(2)当m,n取何值时,函数图象经过原点?
(3)当m,n取何值时,函数图象与y轴交点在x轴上方?
(4)若图象经过一、三、四象限,求m,n的取值范围?
【答案】(1)m>2,n为全体实数;(2)m≠2,n=0,(3)n>0,m≠2,(4)m>2,n<0.
【解析】试题分析:
(1)由一次函数y=(2m-4)x+3n中y随x的增大而增大可得:2m-4>0,3n为任意实数即可求得对应的m、n的取值范围;
(2)由一次函数y=(2m-4)x+3n的图象过原点可得:2m-4![]() 0,3n=0,由此即可求得对应的m、n的取值范围;
0,3n=0,由此即可求得对应的m、n的取值范围;
(3)由一次函数y=(2m-4)x+3n的图象与y轴的交点在x轴上方可得:2m-4![]() 0,3n>0,由此即可解得对应的m,n的取值范围;
0,3n>0,由此即可解得对应的m,n的取值范围;
(4)由一次函数y=(2m-4)x+3n的图象过第一、三、四象限可得:2m-4>0,3n<0,由此即可求得对应的m,n的取值范围.
试题解析:
由题意可知:k=2m-4,b=3n,
(1)∵y随x的增大而增大,
∴k>0,b为任意实数,
∴2m-4>0,3n为任意实数,
∴m>2,n为全体实数;
(2)∵函数图象经过原点,
∴k≠0,b=0,即2m-4≠0,3n=0,
∴m≠2,n=0;
(3)∵函数图象与y轴交点在x轴上方,
∴b>0,k≠0,即3n>0,2m-4≠0,
∴n>0,m≠2;
(4)∵图象经过一、三、四象限,求m,n的取值范围,
∴k>0,b<0,即2m-4>0,3n<0,
∴m>2,n<0.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】某学校为了解七年级男生体质健康情况,随机抽取若干名男生进行测试,测试结果分为优秀、良好、合格、不合格四个等级,统计整理数据并绘制图1、图2两幅不完整的统计图,请根据图中信息回答下列问题:

(1)本次接收随机抽样调查的男生人数为 人,扇形统计图中“良好”所对应的圆心角的度数为 ;
(2)补全条形统计图中“优秀”的空缺部分;
(3)若该校七年级共有男生480人,请估计全年级男生体质健康状况达到“良好”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线l1∥l2,且l3和l1,l2分别相交于A,B两点,l4和l1,l2分别交于C,D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3,
点P在线段AB上.
(1)若∠1=22°,∠2=33°,则∠3=________;
(2)试找出∠1,∠2,∠3之间的等量关系,并说明理由;
(3)应用(2)中的结论解答下列问题;
如图②,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数;
(4)如果点P在直线l3上且在A,B两点外侧运动时,其他条件不变,试探究∠1,∠2,∠3之间的关系(点P和A,B两点不重合),直接写出结论即可.



查看答案和解析>>
科目:初中数学 来源: 题型:
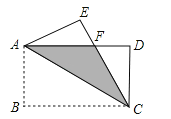
【题目】如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
(1)求证:△AFE≌△CDF;
(2)若AB=4,BC=8,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,H为BC上一点,且BH=BA交AC于点F,连接FH.
⑴求证:AE=FH;
⑵作EG//BC交AC于点G若AG=5,AC=8,求FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.其中正确结论的序号是( )

A. ②④ B. ①③ C. ②③④ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com