
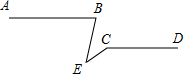
 如图,AB∥CD,请探索∠B,∠C,∠E的关系?
如图,AB∥CD,请探索∠B,∠C,∠E的关系? 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上,如果用(1,0)表示C点的位置,用(4,1)表示B点的位置,那么.
如图,方格纸中每个小正方形的边长都是1,△ABC的三个顶点都在格点上,如果用(1,0)表示C点的位置,用(4,1)表示B点的位置,那么.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一次函数经过点A(-2,-1),B(1,3)两点,该函数表示的直线交x轴于点C交y轴于点D
一次函数经过点A(-2,-1),B(1,3)两点,该函数表示的直线交x轴于点C交y轴于点D查看答案和解析>>
科目:初中数学 来源: 题型:解答题
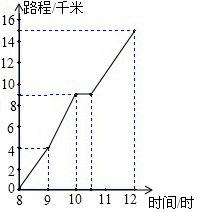 如图为一位旅行者在早晨8时从城市出发到郊外所走的路程S(单位:千米)与时间t(单位:时)的变量关系的图象.根据图象回答问题:
如图为一位旅行者在早晨8时从城市出发到郊外所走的路程S(单位:千米)与时间t(单位:时)的变量关系的图象.根据图象回答问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (5,2) | B. | (5,3) | C. | (6,2) | D. | (6,5) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 记录 | 天平左边 | 天平右边 | 天平状态 |
| 记录一 | 2枚1元硬币和7枚5角硬币 | 4个10克砝码 | 平衡 |
| 记录二 | 15枚1元硬币 | 20枚5角硬币和1个10克砝码 | 平衡 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com