
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 交
交![]() 于点
于点![]() ,切线
,切线![]() 交
交![]() 于点
于点![]() .
.
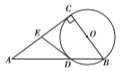
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD.只要证明∠A+∠B=90°,∠ADE+∠B=90°即可解决问题;
(2)首先证明AC=2DE=20.在Rt△ADC中,由勾股定理得到DC的长,设BD=x.在Rt△BDC中,BC2=x2+122.在Rt△ABC中,BC2=(x+16)2﹣202,可得x2+122=(x+16)2﹣202,解方程即可解决问题.
(1)连接OD.
∵DE是切线,∴∠ODE=90°,∴∠ADE+∠BDO=90°.
∵∠ACB=90°,∴∠A+∠B=90°.
∵OD=OB,∴∠B=∠BDO,∴∠ADE=∠A.
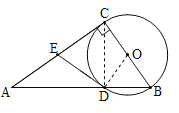
(2)连接CD.
∵∠ADE=∠A,∴AE=DE.
∵BC是⊙O的直径,∠ACB=90°,
∴EC是⊙O的切线,∴ED=EC,∴AE=EC.
∵DE=10,∴AC=2DE=20,
在Rt△ADC中,DC![]() 12,
12,
设BD=x.在Rt△BDC中,BC2=x2+122.
在Rt△ABC中,BC2=(x+16)2﹣202,
∴x2+122=(x+16)2﹣202,
解得x=9,∴BC![]() 15.
15.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】中华文明,源远流长,中华汉字,寓意深广.为传承中华优秀传统文化,某中学德育处组织了一次全校2000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,学校德育处随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩x(分)分数段 | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | 0.2 |
80≤x<90 | m | 0.35 |
90≤x<100 | 50 | n |
频数分布直方图

根据所给的信息,回答下列问题:
(1)m=________;n=________;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在________分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的2000名学生中成绩是“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
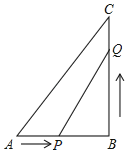
【题目】如图,在Rt△ABC中,∠B=90°,AB=5cm,BC=7cm.点P从点A开始沿AB边向终点B以1cm/s的速度移动,点Q从点B开始沿BC边向终点C以2cm/s的速度移动,当其中一点到达终点时,另一点随之停止.点P,Q分别从点A,B同时出发.
(1)求出发多少秒时PQ的长度等于5cm;
(2)出发 秒时,△BPQ中有一个角与∠A相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+bx+c的顶点为C,对称轴为直线x=1,且经过点A(3,-1),与y轴交于点B.
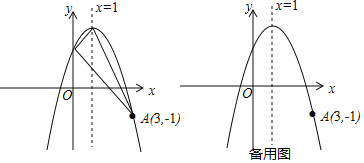
(1)求抛物线的解析式;
(2)判断△ABC的形状,并说明理由;
(3)经过点A的直线交抛物线于点P,交x轴于点Q,若S△OPA=2S△OQA,试求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数![]() 的图象经过原点,开口向上,对称轴为直线
的图象经过原点,开口向上,对称轴为直线![]() ,对于下列两个结论:①m为任意实数,则有
,对于下列两个结论:①m为任意实数,则有![]() ;②方程
;②方程![]() 有两个不相等的实数根,一个根小于0,另一个根大于2,说法正确的是( )
有两个不相等的实数根,一个根小于0,另一个根大于2,说法正确的是( )
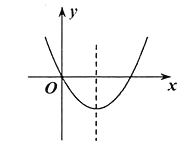
A.①对,②错B.①错,②对C.①②都对D.①②都错
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点E在边
中,点E在边![]() 上,将点E绕点D逆时针旋转得到点F,若点F恰好落在边
上,将点E绕点D逆时针旋转得到点F,若点F恰好落在边![]() 的延长线上,连接
的延长线上,连接![]() ,
,![]() ,
,![]() .
.
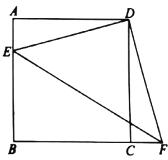
(1)判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)若![]() ,则
,则![]() 的面积为________.
的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
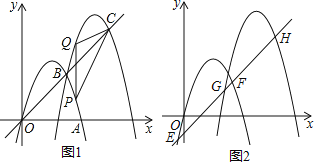
【题目】如图1,抛物线M1:y=﹣x2+4x交x正半轴于点A,将抛物线M1先向右平移3个单位,再向上平移3个单位得到抛物线M2,M1与M2交于点B,直线OB交M2于点C.
(1)求抛物线M2的解析式;
(2)点P是抛物线M1上AB间的一点,作PQ⊥x轴交抛物线M2于点Q,连接CP,CQ.设点P的横坐标为m,当m为何值时,使△CPQ的面积最大,并求出最大值;
(3)如图2,将直线OB向下平移,交抛物线M1于点E,F,交抛物线M2于点G,H,则![]() 的值是否为定值,证明你的结论.
的值是否为定值,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年郑州市初中体育学业水平考试实行改革,增加了两类自选类项目:一类是运动技能测试,学生可以从篮球、足球、排球向上垫球三个项目中必须自选一项;另一类是身体力量测试,学生从一分钟跳绳、仰卧起坐(女)或引体向上(男)、原地正面掷实心球、立定跳远四个项目中再选一项,则某一初三男学生同时选择篮球和立定跳远这两项的概率是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com