
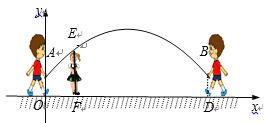
【题目】跳绳时,绳甩到最高处时的形状是抛物线. 正在甩绳的甲、乙两名同学拿绳的手间距AB为6米,到地面的距离AO和BD均为0. 9米,身高为1. 4米的小丽站在距点O的水平距离为1米的点F处,绳子甩到最高处时刚好通过她的头顶点E. 以点O为原点建立如图所示的平面直角坐标系, 设此抛物线的解析式为![]() .
.
(1)求该抛物线的解析式;
(2)如果身高为1. 85米的小华也想参加跳绳,问绳子能否顺利从他头顶越过?请说明理由;
(3)如果一群身高在1. 4米到1. 7米之间的人站在OD之间,且离点O的距离为t米, 绳子甩到最高处时必须超过他们的头顶,请结合图像,写出t的取值范围_______________.
【答案】(1)![]() ;(2)绳子不能顺利从他头顶越过;(3)1<t<5.
;(2)绳子不能顺利从他头顶越过;(3)1<t<5.
【解析】
(1)选定抛物线上两点E(1,1.4),B(6,0.9)坐标代入求出解析式即可;
(2)将函数解析式配方成顶点式,得到函数的最大值,据此即可作出判断;
(3)实质上就是求y=1.4时,对应的x的两个值,就是t的取值范围.
解:(1)由题意得点E(1,1.4),B(6,0.9),代入![]() 得
得
![]() ,解得:
,解得: ![]() ,
,
∴所求的抛物线的解析式是![]() ;
;
(2)∵![]() ,
,
∵![]() ,
,
∴x=3时,y有最大值为1.8,
∵1.85>1.8,
∴绳子不能顺利从他头顶越过;
(3)身高在1. 4米到1. 7米之间的人站在OD之间,
∵1.4<1.7<1.8,
∴只需要计算1.4米身高的情况.
当y=1.4时,![]() ,
,
解得![]() ,
,
∴1<t<5,故答案为:1<t<5.


科目:初中数学 来源: 题型:
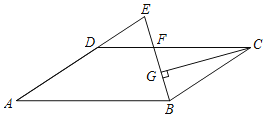
【题目】如图,在ABCD中,AB=18,AD=12,∠ABC的平分线交CD于点F,交AD的延长线于点E,CG⊥BE,垂足为G,若EF=4,则线段CG的长为( )
A.2![]() B.6
B.6![]() C.4
C.4![]() D.8
D.8![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如图所示(收支差额
的函数关系如图所示(收支差额![]() 车票收入
车票收入![]() 支出费 用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用.下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则下列说法正确的是:
支出费 用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用.下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则下列说法正确的是:
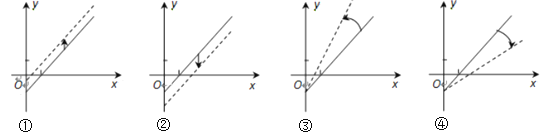
A. ①反映了建议(Ⅱ),③反映了建议(Ⅰ) B. ②反映了建议(Ⅰ),④反映了建议(Ⅱ)
C. ①反映了建议(Ⅰ),③反映了建议(Ⅱ) D. ②反映了建议(Ⅱ),④反映了建议(Ⅰ)
查看答案和解析>>
科目:初中数学 来源: 题型:
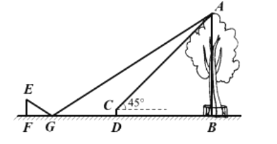
【题目】小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示。于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动带点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米。已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB。(小平面镜的大小忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
①abc<0;②b>2a;③a+b+c=0;④8a+c>0;⑤ax2+bx+c=0的两根分别为﹣3和1.
其中正确的命题有( )
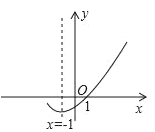
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+4x+c经过A(2,0)、B(0,﹣6)两点,其对称轴与x轴交于点C.
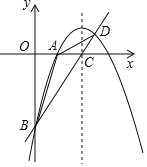
(1)求该抛物线和直线BC的解析式;
(2)设抛物线与直线BC相交于点D,求△ABD的面积;
(3)在该抛物线的对称轴上是否存在点Q,使得△QAB的周长最小?若存在,求出Q点的坐标及△QAB最小周长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小蒲家与学校之间是一条笔直的公路,小蒲从家步行前往学校的途中发现忘带作业本,便向路人借了手机打给妈妈,妈妈接到电话后,带上作业本马上赶往学校,同时小蒲沿原路返回,两人相遇后,小蒲立即赶往学校,妈妈沿原路返回家,小蒲到达学校刚好比妈妈到家晩了2分钟.若小蒲步行的速度始终不变,打电话和交接作业本的时间忽略不计,小蒲和妈妈之间的距离y米与小蒲打完电话后步行的时间x分钟之间的函数关系如图所示;则相遇后妈妈返回家的速度是每分钟_____米.
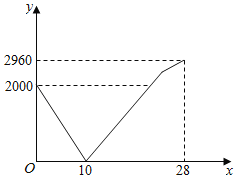
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com