
【题目】小明利用刚学过的测量知识来测量学校内一棵古树的高度。一天下午,他和学习小组的同学带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示。于是他们先在古树周围的空地上选择一点D,并在点D处安装了测量器DC,测得古树的顶端A的仰角为45°;再在BD的延长线上确定一点G,使DG=5米,并在G处的地面上水平放置了一个小平面镜,小明沿着BG方向移动,当移动带点F时,他刚好在小平面镜内看到这棵古树的顶端A的像,此时,测得FG=2米,小明眼睛与地面的距离EF=1.6米,测倾器的高度CD=0.5米。已知点F、G、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,求这棵古树的高度AB。(小平面镜的大小忽略不计)
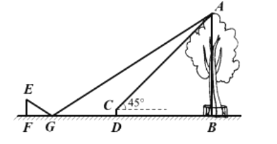
【答案】这棵古树的高AB为18m.
【解析】
如图,过点C作CH⊥AB于点H,则CH=BD,BH=CD=0.5,继而可得AB=BD+0.5,再证明△EFG∽△ABC,根据相似三角形的性质得![]() ,即
,即![]() ,由此求得BD长,即可求得AB长.
,由此求得BD长,即可求得AB长.
如图,过点C作CH⊥AB于点H,
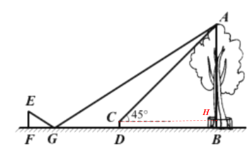
则CH=BD,BH=CD=0.5,
在Rt△ACH中,∠ACH=45°,
∴AH=CH=BD,
∴AB=AH+BH=BD+0.5,
∵EF⊥FB,AB⊥FB,
∴∠EFG=∠ABG=90°,
由题意,易知∠EGF=∠AGB,
∴△EFG∽△ABG,
∴![]() ,即
,即![]() ,
,
解得:BD=17.5,
∴AB=17.5+0.5=18(m),
∴这棵古树的高AB为18m.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】某电视台为了解本地区电视节目的收视情况,对部分市民开展了“你最喜爱的电视节目”的问卷调查(每人只填写一项),根据收集的数据绘制了两幅不完整的统计图(如图所示),根据要求回答下列问题:
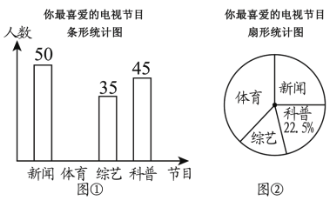
(1)本次问卷调查共调查了________名观众;图②中最喜爱“新闻节目”的人数占调查总人数的百分比为________;
(2)补全图①中的条形统计图;
(3)现有最喜爱“新闻节目”(记为![]() ),“体育节目”(记为
),“体育节目”(记为![]() ),“综艺节目”(记为
),“综艺节目”(记为![]() ),“科普节目”(记为
),“科普节目”(记为![]() )的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“
)的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“![]() ”和“
”和“![]() ”两位观众的概率.
”两位观众的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都市为了扎实推进精准扶贫工作,出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为A,B,C,D类贫困户,为检查帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成如图两幅不完整的统计图.请根据图中信息,回答下列问题:
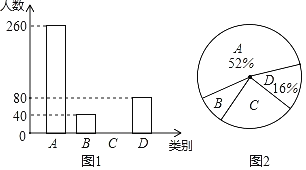
(1)本次抽样调查了多少户贫困户?
(2)成都市共有9100户贫困户,请估计至少得到4种帮扶措施的大约有多少户?
(3)2020年是精准扶贫攻关年,为更好地做好工作,现准备从D类贫困户中的甲、乙、丙、丁四户中随机选取两户进行试点帮扶,请用树状图或列表法求出恰好选中乙和丙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①HE=HF;②EC平分∠DCH;③线段BF的取值范围为3≤BF≤4;④当点H与点A重合时,EF=2![]() .以上结论中,你认为正确的有( )个.
.以上结论中,你认为正确的有( )个.
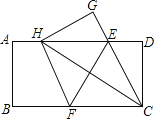
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
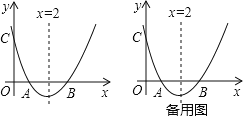
(1)求抛物线的函数表达式;
(2)设D为抛物线的顶点,连接DA、DB,试判断△ABD的形状,并说明理由;
(3)设P为对称轴上一动点,要使PC﹣PB的值最大,求出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=4,BC=5,∠ABC=60°. 按以下步骤作图:①以C为圆心,以适当长为半径做弧,交CB、CD于M、N两点;②分别以M、N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点E,作射线CE交BD于点O,交AD边于点F;则BO的长度为( )
MN的长为半径作弧,两弧相交于点E,作射线CE交BD于点O,交AD边于点F;则BO的长度为( )
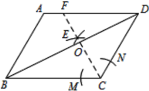
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,单位长度为1的网格坐标系中,一次函数 ![]() 与坐标轴交于A、B两点,反比例函数
与坐标轴交于A、B两点,反比例函数![]() (x>0)经过一次函数上一点C(2,a).
(x>0)经过一次函数上一点C(2,a).
(1)求反比例函数解析式,并用平滑曲线描绘出反比例函数图像;
(2)依据图像直接写出当![]() 时不等式
时不等式![]() 的解集;
的解集;
(3)若反比例函数![]() 与一次函数
与一次函数![]() 交于C、D两点,使用直尺与2B铅笔构造以C、D为顶点的矩形,且使得矩形的面积为10.
交于C、D两点,使用直尺与2B铅笔构造以C、D为顶点的矩形,且使得矩形的面积为10.
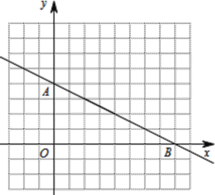

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 边上,
边上,![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
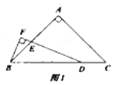
(1)如图1,当![]() 时:①
时:①![]() 的度数为__________;②求证;
的度数为__________;②求证;![]() ;
;
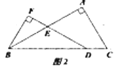
(2)如图2,当![]() 时,求
时,求![]() 的值(用含
的值(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场秋季计划购进一批进价为每件40元的![]() 恤进行销售.
恤进行销售.
(1)根据销售经验,应季销售时,若每件![]() 恤的售价为60元,可售出400件;若每件
恤的售价为60元,可售出400件;若每件![]() 恤的售价每提高1元,销售量相应减少10件.
恤的售价每提高1元,销售量相应减少10件.
①假设每件![]() 恤的售价提高
恤的售价提高![]() 元,那么销售每件
元,那么销售每件![]() 恤所获得的利润是 元,销售量是 件(用含
恤所获得的利润是 元,销售量是 件(用含![]() 的代数式表示);
的代数式表示);
②设应季销售利润为![]() 元,请写
元,请写![]() 与
与![]() 的函数关系式;并求出应季销售利润为8000元时每件
的函数关系式;并求出应季销售利润为8000元时每件![]() 恤的售价.
恤的售价.
(2)根据销售经验,过季处理时,若每件![]() 恤的售价定为30元亏本销售,可售出50件;若每件
恤的售价定为30元亏本销售,可售出50件;若每件![]() 恤的售价每降低1元,销售量相应增加5条.
恤的售价每降低1元,销售量相应增加5条.
①若剩余100件![]() 恤需要处理,经过降价处理后还是无法销售的只能积压在仓库,损失本金;若使亏损金额最小,每件
恤需要处理,经过降价处理后还是无法销售的只能积压在仓库,损失本金;若使亏损金额最小,每件![]() 恤的售价应是多少元?
恤的售价应是多少元?
②若过季需要处理的![]() 恤共
恤共![]() 件,且
件,且![]() ,季亏损金额最小是 元(用含
,季亏损金额最小是 元(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com