
����Ŀ���ɶ���Ϊ����ʵ�ƽ�����ƶ��������̨���������ס�ҽ����ƶ��������������ҵ���֡������йܺ��ذ�Ǩ�����ְ����ʩ��ÿ��ƶ������������2��5�ְ����ʩ���ְ�������2�֡�3�֡�4�ֺ�5�ְ����ʩ��ƶ�����ֱ��ΪA��B��C��D��ƶ������Ϊ�������ʩ�Ƿ���ʵ�������ȡ������ƶ�������е��飬�ֽ��ռ������ݻ��Ƴ���ͼ������������ͳ��ͼ�������ͼ����Ϣ���ش��������⣺
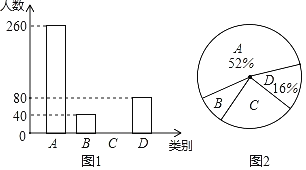
��1�����γ��������˶��ٻ�ƶ������
��2���ɶ��й���9100��ƶ��������������ٵõ�4�ְ����ʩ�Ĵ�Լ�ж��ٻ���
��3��2020���Ǿ���ƶ�����꣬Ϊ���õ����ù�����������D��ƶ�����еļס��ҡ��������Ļ������ѡȡ���������Ե�����������״ͼ���б������ǡ��ѡ���Һͱ��ĸ��ʣ�
���𰸡���1��500������2��3640������3����״ͼ��������![]()
��������
��1����A������������Ӧ�ٷֱȿɵô𰸣�
��2�����ٵõ�4�ְ����ʩ��C��D������������C��D��Ӧ�ٷֱȵĺͣ����ɵõ��𰸣�
��3������״ͼ���б������еȿ��ܵĽ���оٳ��������ø��ʹ�ʽ��⼴�ɣ�
�⣺��1�����γ���������ܻ���Ϊ260��52%��500��������
��2�����B��ƶ������ռ���γ���������ܻ����İٷ���Ϊ��![]() ��100%��8%��
��100%��8%��
���C��ƶ������ռ���γ���������ܻ����İٷ���Ϊ��1��52%��16%��8%��24%��
�������ٵõ�4������ʩ�Ĵ�Լ��9100����24%+16%����3640��������
��3������״ͼ���£�
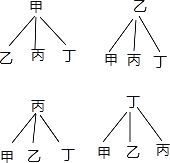
����״ͼ֪����12�ֿ��ܽ��������ǡ��ѡ���Һͱ�����2�ֽ����
����ǡ��ѡ���Һͱ��ĸ���Ϊ![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽��
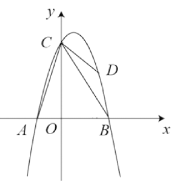
��ͼ��������![]() ������A(-2,0)��B(4,0)���㣬��
������A(-2,0)��B(4,0)���㣬��![]() �ύ�ڵ�C����D����������һ�����㣬���D�ĺ�����Ϊ
�ύ�ڵ�C����D����������һ�����㣬���D�ĺ�����Ϊ![]() .����AC��BC��DB��DC��
.����AC��BC��DB��DC��
(1)�������ߵĺ�������ʽ��
(2)��BCD�����������AOC�������![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
(3)��(2)�������£�����M��![]() ���ϵ�һ�����㣬��N����������һ���㣬���ж��Ƿ���������ĵ�M,ʹ���Ե�B��D��M��NΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����M�����ꣻ�������ڣ���˵������.
���ϵ�һ�����㣬��N����������һ���㣬���ж��Ƿ���������ĵ�M,ʹ���Ե�B��D��M��NΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����M�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
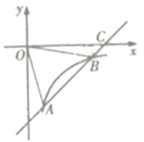
����Ŀ����ͼ����֪һ�κ���y= kx +b��ͼ����������![]() ��ͼ���ڵ�A(2��-4)�͵�B(h��-2)����x���ڵ�C��
��ͼ���ڵ�A(2��-4)�͵�B(h��-2)����x���ڵ�C��
(1)�������������Ľ���ʽ��
(2)����QA��OB�����AOB�������
(3)��ֱ��д������ʽ![]() �Ľ⼯��
�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�ڰٻ��̳�������A��B����Ʒ�Ƶ�������AƷ��������2400Ԫ������BƷ��������1950Ԫ���ҹ���AƷ�����������ǹ���BƷ������������2������֪����һ��BƷ������ȹ���һ��AƷ������50Ԫ��
��1������һ��AƷ�ơ�һ��BƷ�Ƶ�����������Ԫ��
��2����ѧУ�����ٴι���A��B����Ʒ������30����ǡ��ٻ��̳�������Ʒ��������ۼ۽��е�����AƷ�������ۼ۱ȵ�һ�ι���ʱ�����10%��BƷ������һ�ι���ʱ�ۼ۵�9�۳��ۣ����������ѧ�˴ι���A��B����Ʒ��������ܷ��ò�����3200Ԫ����ô��ѧУ�˴����ɹ�����ٸ�BƷ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
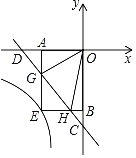
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y����x��2��x�ᣬy��ֱ��ڵ�D��C����G��H���߶�CD�ϵ��������㣬�ҡ�GOH��45��������G��GA��x����A������H��HB��y����B���ӳ�AG��BH���ڵ�E�������E�ķ���������y��![]() �Ľ���ʽΪ_____��
�Ľ���ʽΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ƽ���ı���ABCD�У��Խ���AC��BD���ڵ�O����E��DB�ӳ����ϵ�һ�㣬��EA��EC���ֱ��ӳ�AD��EC���ڵ�F��
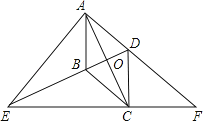
��1����֤���ı���ABCDΪ���Σ�
��2�������AEC��2��BAC����֤��ECCF��AFAD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
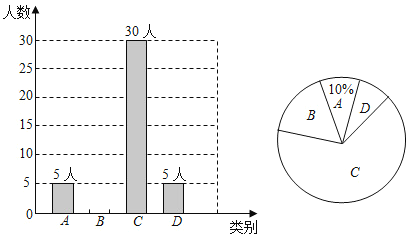
����Ŀ������������ӽ���������������ܵ����㷺��ע�������ijУ��ѧ��ϲ�����������������飬���ռ�����Ϣ����ͳ�ƣ����������������в�������ͳ��ͼ���������ͳ��ͼ���ṩ����Ϣ������������⣺
ͼ��A��ʾ����ϲ������B��ʾ��ϲ������C��ʾ��һ������D��ʾ����ϲ����
��1���˴γ������飬�������� ��ѧ����
��2����ͼ1�е�����ͳ��ͼ����������
��3��ͼ2�У�C�����������ε�Բ�Ľ�Ϊ �ȣ�
��4������У����ѧ��1800�ˣ����Ƹ�Уѧ����D���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
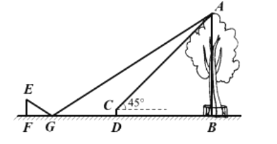
����Ŀ��С�����ø�ѧ���IJ���֪ʶ������ѧУ��һ�ù����ĸ߶ȡ�һ�����磬����ѧϰС���ͬѧ���Ų�������������ù���ǰ��������Χ����������������������ĵײ�B����ͼ��ʾ�������������ڹ�����Χ�Ŀյ���ѡ��һ��D�����ڵ�D����װ�˲�����DC����ù����Ķ���A������Ϊ45��������BD���ӳ�����ȷ��һ��G��ʹDG=5�ף�����G���ĵ�����ˮƽ������һ��Сƽ�澵��С������BG�����ƶ������ƶ�����Fʱ�����պ���Сƽ�澵�ڿ�����ù����Ķ���A����ʱ�����FG=2�ף�С���۾������ľ���EF=1.6�ף��������ĸ߶�CD=0.5�ס���֪��F��G��D��B��ͬһˮƽֱ���ϣ���EF��CD��AB����ֱ��FB������ù����ĸ߶�AB����Сƽ�澵�Ĵ�С���Բ��ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�����ı���ABCD�У���DAB���Խ���ACƽ�֣���AC2=AB��AD�����dzƸ��ı���Ϊ���ɷ��ı��Ρ�����DAB��Ϊ���ɷֽǡ���
��1����ͼ2���ı���ABCDΪ���ɷ��ı��Ρ�����DABΪ���ɷֽǡ��������DCB=��DAB�����DAB=_________��
��2����ͼ3�����ı���ABCD�У���DAB=60�㣬ACƽ�֡�DAB���ҡ�BCD=150�㣬��֤���ı���ABCDΪ���ɷ��ı��Ρ���
��3�������ı���ABCDΪ���ɷ��ı��Ρ�����DABΪ���ɷֽǡ�����AC=4��BC=2����D=90�㣬��AD�ij�?

ͼ1 ͼ2 ͼ3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com