
ЁОЬтФПЁПзлКЯгыЬНОП
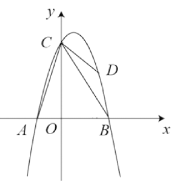
ШчЭМЃЌХзЮяЯп![]() ОЙ§ЕуA(-2,0)ЃЌB(4,0)СНЕуЃЌгы
ОЙ§ЕуA(-2,0)ЃЌB(4,0)СНЕуЃЌгы![]() жсНЛгкЕуCЃЌЕуDЪЧХзЮяЯпЩЯвЛИіЖЏЕуЃЌЩшЕуDЕФКсзјБъЮЊ
жсНЛгкЕуCЃЌЕуDЪЧХзЮяЯпЩЯвЛИіЖЏЕуЃЌЩшЕуDЕФКсзјБъЮЊ![]() .СЌНгACЃЌBCЃЌDBЃЌDCЃЌ
.СЌНгACЃЌBCЃЌDBЃЌDCЃЌ
(1)ЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
(2)ЁїBCDЕФУцЛ§ЕШгкЁїAOCЕФУцЛ§ЕФ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
(3)дк(2)ЕФЬѕМўЯТЃЌШєЕуMЪЧ![]() жсЩЯЕФвЛИіЖЏЕуЃЌЕуNЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЪдХаЖЯЪЧЗёДцдкетбљЕФЕуM,ЪЙЕУвдЕуBЃЌDЃЌMЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌШєДцдкЃЌЧыжБНгаДГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
жсЩЯЕФвЛИіЖЏЕуЃЌЕуNЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЪдХаЖЯЪЧЗёДцдкетбљЕФЕуM,ЪЙЕУвдЕуBЃЌDЃЌMЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌШєДцдкЃЌЧыжБНгаДГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЁОД№АИЁП(1)![]() ЃЛ(2)3ЃЛ(3)
ЃЛ(2)3ЃЛ(3)![]() .
.
ЁОНтЮіЁП
(1)РћгУД§ЖЈЯЕЪ§ЗЈНјааЧѓНтМДПЩЃЛ
(2)зїжБЯпDEЁЭ![]() жсгкЕуEЃЌНЛBCгкЕуGЃЌзїCFЁЭDEЃЌДЙзуЮЊFЃЌЯШЧѓГіSЁїOAC=6ЃЌдйИљОнSЁїBCD=
жсгкЕуEЃЌНЛBCгкЕуGЃЌзїCFЁЭDEЃЌДЙзуЮЊFЃЌЯШЧѓГіSЁїOAC=6ЃЌдйИљОнSЁїBCD=![]() SЁїAOCЃЌЕУЕНSЁїBCD =
SЁїAOCЃЌЕУЕНSЁїBCD =![]() ЃЌШЛКѓЧѓГіBCЕФНтЮіЪНЮЊ
ЃЌШЛКѓЧѓГіBCЕФНтЮіЪНЮЊ![]() ЃЌдђПЩЕУЕуGЕФзјБъЮЊ
ЃЌдђПЩЕУЕуGЕФзјБъЮЊ![]() ЃЌгЩДЫПЩЕУ
ЃЌгЩДЫПЩЕУ![]() ЃЌдйИљОнSЁїBCD=SЁїCDG+SЁїBDG=
ЃЌдйИљОнSЁїBCD=SЁїCDG+SЁїBDG=![]() ЃЌПЩЕУЙигкmЕФЗНГЬЃЌНтЗНГЬМДПЩЧѓЕУД№АИЃЛ
ЃЌПЩЕУЙигкmЕФЗНГЬЃЌНтЗНГЬМДПЩЧѓЕУД№АИЃЛ
(3)ДцдкЃЌШчЯТЭМЫљЪОЃЌвдBDЮЊБпЛђепвдBDЮЊЖдНЧЯпНјааЦНааЫФБпаЮЕФЙЙЭМЃЌвдBDЮЊБпЪБЃЌга3жжЧщПіЃЌгЩЕуDЕФзјБъПЩЕУЕуNЕузнзјБъЮЊЁР![]() ЃЌШЛКѓЗжЕуNЕФзнзјБъЮЊ
ЃЌШЛКѓЗжЕуNЕФзнзјБъЮЊ![]() КЭЕуNЕФзнзјБъЮЊ
КЭЕуNЕФзнзјБъЮЊ![]() СНжжЧщПіЗжБ№ЧѓНтЃЛвдBDЮЊЖдНЧЯпЪБЃЌга1жжЧщПіЃЌДЫЪБN1ЕугыN2ЕужиКЯЃЌИљОнЦНааЫФБпаЮЕФЖдБпЦНааЧвЯрЕШПЩЧѓЕУBM1=N1D=4ЃЌМЬЖјЧѓЕУOM1= 8ЃЌгЩДЫМДПЩЧѓЕУД№АИ.
СНжжЧщПіЗжБ№ЧѓНтЃЛвдBDЮЊЖдНЧЯпЪБЃЌга1жжЧщПіЃЌДЫЪБN1ЕугыN2ЕужиКЯЃЌИљОнЦНааЫФБпаЮЕФЖдБпЦНааЧвЯрЕШПЩЧѓЕУBM1=N1D=4ЃЌМЬЖјЧѓЕУOM1= 8ЃЌгЩДЫМДПЩЧѓЕУД№АИ.
(1)ХзЮяЯп![]() ОЙ§ЕуA(-2,0)ЃЌB(4,0)ЃЌ
ОЙ§ЕуA(-2,0)ЃЌB(4,0)ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ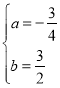 ЃЌ
ЃЌ
ЁрХзЮяЯпЕФКЏЪ§БэДяЪНЮЊ![]() ЃЛ
ЃЛ
(2)зїжБЯпDEЁЭ![]() жсгкЕуEЃЌНЛBCгкЕуGЃЌзїCFЁЭDEЃЌДЙзуЮЊFЃЌ
жсгкЕуEЃЌНЛBCгкЕуGЃЌзїCFЁЭDEЃЌДЙзуЮЊFЃЌ
ЁпЕуAЕФзјБъЮЊ(-2,0)ЃЌЁрOA=2ЃЌ
гЩ![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌЁрЕуCЕФзјБъЮЊ(0,6)ЃЌЁрOC=6ЃЌ
ЃЌЁрЕуCЕФзјБъЮЊ(0,6)ЃЌЁрOC=6ЃЌ
ЁрSЁїOAC=![]() ЃЌ
ЃЌ
ЁпSЁїBCD=![]() SЁїAOCЃЌ
SЁїAOCЃЌ
ЁрSЁїBCD =![]() ЃЌ
ЃЌ
ЩшжБЯпBCЕФКЏЪ§БэДяЪНЮЊ![]() ЃЌ
ЃЌ
гЩBЃЌCСНЕуЕФзјБъЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ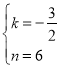 ЃЌ
ЃЌ
ЁржБЯпBCЕФКЏЪ§БэДяЪНЮЊ![]() ЃЌ
ЃЌ
ЁрЕуGЕФзјБъЮЊ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпЕуBЕФзјБъЮЊ(4,0)ЃЌЁрOB=4ЃЌ
ЁпSЁїBCD=SЁїCDG+SЁїBDG=![]() ЃЌ
ЃЌ
ЁрSЁїBCD =![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУ![]() (Щс)ЃЌ
(Щс)ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЕФжЕЮЊ3ЃЛ
ЕФжЕЮЊ3ЃЛ
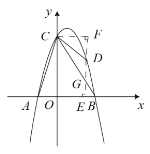
(3)ДцдкЃЌШчЯТЭМЫљЪОЃЌвдBDЮЊБпЛђепвдBDЮЊЖдНЧЯпНјааЦНааЫФБпаЮЕФЙЙЭМЃЌ
вдBDЮЊБпЪБЃЌга3жжЧщПіЃЌ
ЁпDЕузјБъЮЊ![]() ЃЌЁрЕуNЕузнзјБъЮЊЁР
ЃЌЁрЕуNЕузнзјБъЮЊЁР![]() ЃЌ
ЃЌ
ЕБЕуNЕФзнзјБъЮЊ![]() ЪБЃЌШчЕуN2ЃЌ
ЪБЃЌШчЕуN2ЃЌ
ДЫЪБ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() (Щс)ЃЌ
(Щс)ЃЌ
Ёр![]() ЃЌЁр
ЃЌЁр![]() ЃЛ
ЃЛ
ЕБЕуNЕФзнзјБъЮЊ![]() ЪБЃЌШчЕуN3ЃЌN4ЃЌ
ЪБЃЌШчЕуN3ЃЌN4ЃЌ
ДЫЪБ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]()
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
вдBDЮЊЖдНЧЯпЪБЃЌга1жжЧщПіЃЌДЫЪБN1ЕугыN2ЕужиКЯЃЌ
Ёп![]() ЃЌD(3ЃЌ
ЃЌD(3ЃЌ![]() )ЃЌ
)ЃЌ
ЁрN1D=4ЃЌ
ЁрBM1=N1D=4ЃЌ
ЁрOM1=OB+BM1=8ЃЌ
ЁрM1(8ЃЌ0)ЃЌ
злЩЯЃЌЕуMЕФзјБъЮЊЃК![]() .
.


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
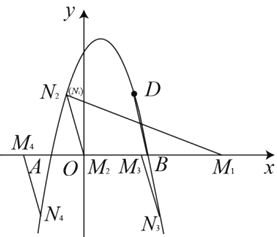
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЮЊ
ЮЊ![]() ЩЯвЛЕуЃЌвд
ЩЯвЛЕуЃЌвд![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ГЄЮЊАыОЖзїдВЃЌгы
ГЄЮЊАыОЖзїдВЃЌгы![]() ЯрЧагкЕу
ЯрЧагкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛ
НЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ,Чв
,Чв![]() .
.
ЃЈ1ЃЉЧѓжЄЃК![]() ЮЊ
ЮЊ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ,Чѓ
,Чѓ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПа§зЊБфЛЛЪЧНтОіЪ§бЇЮЪЬтжавЛжжживЊЕФЫМЯыЗНЗЈЃЌЭЈЙ§а§зЊБфЛЛПЩвдНЋЗжЩЂЕФЬѕМўМЏжаЕНвЛЦ№ЃЌДгЖјЗНБуНтОіЮЪЬтЃЎ
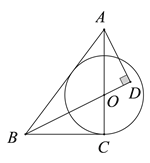
вбжЊЃЌЁїABCжаЃЌABЃНACЃЌЁЯBACЃНІСЃЌЕуDЁЂEдкБпBCЩЯЃЌЧвЁЯDAEЃН![]() ІСЃЎ
ІСЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБІСЃН60ЁуЪБЃЌНЋЁїAECШЦЕуAЫГЪБеыа§зЊ60ЁуЕНЁїAFBЕФЮЛжУЃЌСЌНгDFЃЌ
ЂйЧѓЁЯDAFЕФЖШЪ§ЃЛ
ЂкЧѓжЄЃКЁїADEЁеЁїADFЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБІСЃН90ЁуЪБЃЌВТЯыBDЁЂDEЁЂCEЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌЕБІСЃН120ЁуЃЌBDЃН4ЃЌCEЃН5ЪБЃЌЧыжБНгаДГіDEЕФГЄЮЊЁЁ ЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
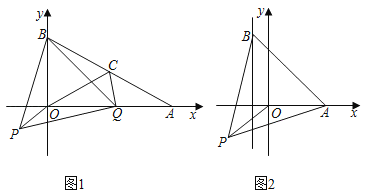
ЁОЬтФПЁПЃЈ1ЃЉЮЪЬтЗЂЯжЃКШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌAЕуЕФзјБъЮЊЃЈ2![]() ЃЌ0ЃЉЃЌЕуBЕФзјБъЮЊЃЈ0ЃЌ2ЃЉЃЌСЌНгABЃЌЕуCЪЧABЕФжаЕуЃЌЕуQЪЧЯпЖЮAOЩЯЕФЖЏЕуЃЌСЌНгOCЁЂCQЃЌвдBQЮЊБпЙЙдьЕШБпЁїBPQЃЌСЌНгOPЁЂPQЃЎЬюПеЃК
ЃЌ0ЃЉЃЌЕуBЕФзјБъЮЊЃЈ0ЃЌ2ЃЉЃЌСЌНгABЃЌЕуCЪЧABЕФжаЕуЃЌЕуQЪЧЯпЖЮAOЩЯЕФЖЏЕуЃЌСЌНгOCЁЂCQЃЌвдBQЮЊБпЙЙдьЕШБпЁїBPQЃЌСЌНгOPЁЂPQЃЎЬюПеЃК
ЂйOPгыCQЕФДѓаЁЙиЯЕЪЧЁЁ ЁЁЃЎ
ЂкOPЕФзюаЁжЕЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉНтОіЮЪЬтЃКдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЕуQдЫЖЏЕФЙ§ГЬжаЕБЁїACQЮЊжБНЧШ§НЧаЮЪБЃЌЧѓOPЕФГЄЃП
ЃЈ3ЃЉЭиеЙЬНОПЃКШчЭМ2ЃЌЕБЕуBЮЊжБЯпxЃНЉ1ЩЯвЛЖЏЕуЃЌЕуAЃЈ2![]() ЃЌ0ЃЉЃЌСЌНгABЃЌвдABЮЊвЛБпЯђЯТзїЕШБпЁїABPЃЌСЌНгOPЃЌЧыжБНгаДГіOPЕФзюаЁжЕЃЎ
ЃЌ0ЃЉЃЌСЌНгABЃЌвдABЮЊвЛБпЯђЯТзїЕШБпЁїABPЃЌСЌНгOPЃЌЧыжБНгаДГіOPЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧФГТЗЕЦдкЧІДЙУцФкЕФЪОвтЭМЃЌЕЦжљACЕФИпЮЊ11УзЃЌЕЦИЫABгыЕЦжљACЕФМаНЧЁЯA=120ЁуЃЌТЗЕЦВЩгУзЖаЮЕЦежЃЌдкЕиУцЩЯЕФееЩфЧјгђDEГЄЮЊ18УзЃЌДгDЃЌEСНДІВтЕУТЗЕЦBЕФбіНЧЗжБ№ЮЊІСКЭІТЃЌЧвtanІС=6ЃЌtanІТ=![]() ЃЌЧѓЕЦИЫABЕФГЄЖШЃЎ
ЃЌЧѓЕЦИЫABЕФГЄЖШЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
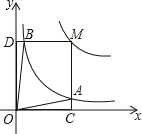
ЁОЬтФПЁПЗДБШР§КЏЪ§yЃН![]() ЃЈaЃО0ЃЌaЮЊГЃЪ§ЃЉКЭyЃН
ЃЈaЃО0ЃЌaЮЊГЃЪ§ЃЉКЭyЃН![]() дкЕквЛЯѓЯоФкЕФЭМЯѓШчЭМЫљЪОЃЌЕуMдкyЃН
дкЕквЛЯѓЯоФкЕФЭМЯѓШчЭМЫљЪОЃЌЕуMдкyЃН![]() ЕФЭМЯѓЩЯЃЌMCЁЭxжсгкЕуCЃЌНЛyЃН
ЕФЭМЯѓЩЯЃЌMCЁЭxжсгкЕуCЃЌНЛyЃН![]() ЕФЭМЯѓгкЕуAЃЛMDЁЭyжсгкЕуDЃЌНЛyЃН
ЕФЭМЯѓгкЕуAЃЛMDЁЭyжсгкЕуDЃЌНЛyЃН![]() ЕФЭМЯѓгкЕуBЃЌЕБЕуMдкyЃН
ЕФЭМЯѓгкЕуBЃЌЕБЕуMдкyЃН![]() ЕФЭМЯѓЩЯдЫЖЏЪБЃЌвдЯТНсТлЃКЂйSЁїODBЃНSЁїOCAЃЛЂкЫФБпаЮOAMBЕФУцЛ§ВЛБфЃЛЂлЕБЕуAЪЧMCЕФжаЕуЪБЃЌдђЕуBЪЧMDЕФжаЕуЃЎЦфжае§ШЗНсТлЪЧЃЈЁЁЁЁЃЉ
ЕФЭМЯѓЩЯдЫЖЏЪБЃЌвдЯТНсТлЃКЂйSЁїODBЃНSЁїOCAЃЛЂкЫФБпаЮOAMBЕФУцЛ§ВЛБфЃЛЂлЕБЕуAЪЧMCЕФжаЕуЪБЃЌдђЕуBЪЧMDЕФжаЕуЃЎЦфжае§ШЗНсТлЪЧЃЈЁЁЁЁЃЉ
A. ЂйЂк B. ЂйЂл C. ЂкЂл D. ЂйЂкЂл
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕчЪгЬЈЮЊСЫНтБОЕиЧјЕчЪгНкФПЕФЪеЪгЧщПіЃЌЖдВПЗжЪаУёПЊеЙСЫЁАФузюЯВАЎЕФЕчЪгНкФПЁБЕФЮЪОэЕїВщЃЈУПШЫжЛЬюаДвЛЯюЃЉЃЌИљОнЪеМЏЕФЪ§ОнЛцжЦСЫСНЗљВЛЭъећЕФЭГМЦЭМЃЈШчЭМЫљЪОЃЉЃЌИљОнвЊЧѓЛиД№ЯТСаЮЪЬтЃК
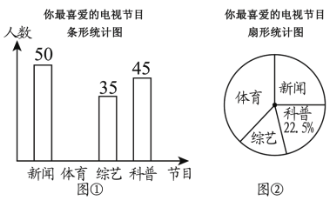
ЃЈ1ЃЉБОДЮЮЪОэЕїВщЙВЕїВщСЫ________УћЙлжкЃЛЭМЂкжазюЯВАЎЁАаТЮХНкФПЁБЕФШЫЪ§еМЕїВщзмШЫЪ§ЕФАйЗжБШЮЊ________ЃЛ
ЃЈ2ЃЉВЙШЋЭМЂйжаЕФЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉЯжгазюЯВАЎЁАаТЮХНкФПЁБЃЈМЧЮЊ![]() ЃЉЃЌЁАЬхг§НкФПЁБЃЈМЧЮЊ
ЃЉЃЌЁАЬхг§НкФПЁБЃЈМЧЮЊ![]() ЃЉЃЌЁАзлвеНкФПЁБЃЈМЧЮЊ
ЃЉЃЌЁАзлвеНкФПЁБЃЈМЧЮЊ![]() ЃЉЃЌЁАПЦЦеНкФПЁБЃЈМЧЮЊ
ЃЉЃЌЁАПЦЦеНкФПЁБЃЈМЧЮЊ![]() ЃЉЕФЙлжкИївЛУћЃЌЕчЪгЬЈвЊДгЫФШЫжаЫцЛњГщШЁСНШЫВЮМгСЊвъЛюЖЏЃЌЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓГіЧЁКУГщЕНзюЯВАЎЁА
ЃЉЕФЙлжкИївЛУћЃЌЕчЪгЬЈвЊДгЫФШЫжаЫцЛњГщШЁСНШЫВЮМгСЊвъЛюЖЏЃЌЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓГіЧЁКУГщЕНзюЯВАЎЁА![]() ЁБКЭЁА
ЁБКЭЁА![]() ЁБСНЮЛЙлжкЕФИХТЪ.
ЁБСНЮЛЙлжкЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГЩЖМЪаЮЊСЫдњЪЕЭЦНјОЋзМЗіЦЖЙЄзїЃЌГіЬЈСЫУёЩњЖЕЕзЁЂвНБЃЭбЦЖЁЂНЬг§ОШжњЁЂВњвЕЗіГжЁЂбјРЯЭаЙмКЭвзЕиАсЧЈетСљжжАяЗіДыЪЉЃЌУПЛЇЦЖРЇЛЇЖМЯэЪмСЫ2ЕН5жжАяЗіДыЪЉЃЌЯжАбЯэЪмСЫ2жжЁЂ3жжЁЂ4жжКЭ5жжАяЗіДыЪЉЕФЦЖРЇЛЇЗжБ№ГЦЮЊAЃЌBЃЌCЃЌDРрЦЖРЇЛЇЃЌЮЊМьВщАяЗіДыЪЉЪЧЗёТфЪЕЃЌЫцЛњГщШЁСЫШєИЩЦЖРЇЛЇНјааЕїВщЃЌЯжНЋЪеМЏЕФЪ§ОнЛцжЦГЩШчЭМСНЗљВЛЭъећЕФЭГМЦЭМЃЎЧыИљОнЭМжааХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
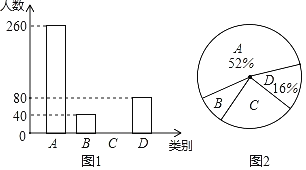
ЃЈ1ЃЉБОДЮГщбљЕїВщСЫЖрЩйЛЇЦЖРЇЛЇЃП
ЃЈ2ЃЉГЩЖМЪаЙВга9100ЛЇЦЖРЇЛЇЃЌЧыЙРМЦжСЩйЕУЕН4жжАяЗіДыЪЉЕФДѓдМгаЖрЩйЛЇЃП
ЃЈ3ЃЉ2020ФъЪЧОЋзМЗіЦЖЙЅЙиФъЃЌЮЊИќКУЕизіКУЙЄзїЃЌЯжзМБИДгDРрЦЖРЇЛЇжаЕФМзЁЂввЁЂБћЁЂЖЁЫФЛЇжаЫцЛњбЁШЁСНЛЇНјааЪдЕуАяЗіЃЌЧыгУЪїзДЭМЛђСаБэЗЈЧѓГіЧЁКУбЁжаввКЭБћЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com