
【题目】某电视台为了解本地区电视节目的收视情况,对部分市民开展了“你最喜爱的电视节目”的问卷调查(每人只填写一项),根据收集的数据绘制了两幅不完整的统计图(如图所示),根据要求回答下列问题:
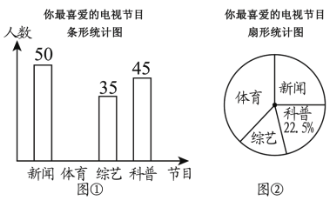
(1)本次问卷调查共调查了________名观众;图②中最喜爱“新闻节目”的人数占调查总人数的百分比为________;
(2)补全图①中的条形统计图;
(3)现有最喜爱“新闻节目”(记为![]() ),“体育节目”(记为
),“体育节目”(记为![]() ),“综艺节目”(记为
),“综艺节目”(记为![]() ),“科普节目”(记为
),“科普节目”(记为![]() )的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“
)的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“![]() ”和“
”和“![]() ”两位观众的概率.
”两位观众的概率.
【答案】(1)![]() ,
,![]() ;(2)补图见解析;(3)恰好抽到最喜爱“
;(2)补图见解析;(3)恰好抽到最喜爱“![]() ”和“
”和“![]() ”两位观众的概率为
”两位观众的概率为![]() .
.
【解析】(1)用喜欢科普节目的人数除以它所占的百分比即可得到调查的总人数,用喜爱“新闻节目”的人数除以调查总人数得到它所占的百分比;
(2)用调查的总人数分别减去喜欢新闻、综艺、科普的人数得到喜欢体育的人数,然后补全图①中的条形统计图;
(3)画树状图展示所有12种等可能的结果数,再找出抽到最喜爱“B”和“C”两位观众的结果数,然后根据概率公式求解.
(1)本次问卷调查共调查的观众数为45÷22.5%=200(人);图②中最喜爱“新闻节目”的人数占调查总人数的百分比为50÷200=25%;
(2)最喜爱“新闻节目”的人数为200-50-35-45=70(人),
如图,
(3)画树状图为:

共有12种等可能的结果数,恰好抽到最喜爱“B”和“C”两位观众的结果数为2,
所以恰好抽到最喜爱“B”和“C”两位观众的概率=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于点C.若tan∠ABC=3,一元二次方程ax2+bx+c=0的两根为﹣8、2.
(1)求二次函数的解析式;
(2)直线l绕点A以AB为起始位置顺时针旋转到AC位置停止,l与线段BC交于点D,P是AD的中点.
①求点P的运动路程;
②如图2,过点D作DE垂直x轴于点E,作DF⊥AC所在直线于点F,连结PE、PF,在l运动过程中,∠EPF的大小是否改变?请说明理由;
(3)在(2)的条件下,连结EF,求△PEF周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个有理数的和等于这两个有理数的积,则称这两个有理数互为相依数.例如:有理数![]() 与3,因为
与3,因为![]() +3=
+3=![]() ×3.所以有理数与
×3.所以有理数与![]() 与3是互为相依数.
与3是互为相依数.
(1)直接判断下列两组有理数是否互为相依数,
①-5与-2;②-3与![]() ;
;
(2)若有理数![]() 与-7 互为相依数,求m的值;
与-7 互为相依数,求m的值;
(3)若有理数a与b互为相依数,b与c互为相反数,求式子5(ab+![]() c)-2(
c)-2(![]() a-b)-4的值;
a-b)-4的值;
(4)对于有理数a(a≠0,1),对它进行如下操作:取a的相依数,得到a1;取a1的倒数,得到a2;取a2的相依数,得到a3;取a3的倒数,得到a4;…,;依次按如上的操作得到一组数a1,a2,a3,…,an , 若a=![]() ,试着直接写出a1,a2,a3,…, a2018的和.
,试着直接写出a1,a2,a3,…, a2018的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为半圆内一点,
为半圆内一点,![]() 为圆心,直径
为圆心,直径![]() 长为
长为![]() ,
,![]() ,
,![]() ,将
,将![]() 绕圆心
绕圆心![]() 逆时针旋转至
逆时针旋转至![]() ,点
,点![]() 在
在![]() 上,则边
上,则边![]() 扫过区域(图中阴影部分)的面积为__________
扫过区域(图中阴影部分)的面积为__________![]() .(结果保留
.(结果保留![]() )
)
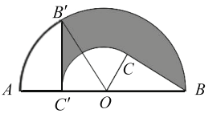
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形![]() 是正方形,
是正方形,![]() 是直线
是直线![]() 上任意一点,
上任意一点,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .当点G在BC边上时(如图1),易证DF-BE=EF.
.当点G在BC边上时(如图1),易证DF-BE=EF.

(1)当点![]() 在
在![]() 延长线上时,在图2中补全图形,写出
延长线上时,在图2中补全图形,写出![]() 、
、![]() 、
、![]() 的数量关系,并证明;
的数量关系,并证明;
(2)当点![]() 在
在![]() 延长线上时,在图3中补全图形,写出
延长线上时,在图3中补全图形,写出![]() 、
、![]() 、
、![]() 的数量关系,不用证明.
的数量关系,不用证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,数![]() 所对应的点与原点的距离叫做数
所对应的点与原点的距离叫做数![]() 的绝对值,记作
的绝对值,记作![]()
提出问题:(1)点![]() 所表示的数如图所示,则
所表示的数如图所示,则![]() 两点间的距离是 ,
两点间的距离是 ,![]() 两点间的距离是_____,
两点间的距离是_____,![]() 两点间的距离是 .
两点间的距离是 .
探究结论:(2)在数轴上,若![]() 两点对应的数分别是
两点对应的数分别是![]() ,则
,则![]() ____ (用含有
____ (用含有![]() 的式子表示).
的式子表示).
拓展应用:(3)请利用.上述结论,解决下列问题:
①![]() 和
和![]() 在数轴上对应的点之间的距离为
在数轴上对应的点之间的距离为
②![]()
③满足![]() 的未知数的值为
的未知数的值为

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家1至6月份的用水量统计如图所示,关于这组数据,下列说法错误的是( ).
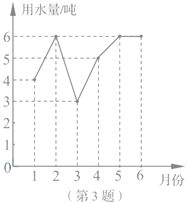
A、众数是6吨 B、平均数是5吨 C、中位数是5吨 D、方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
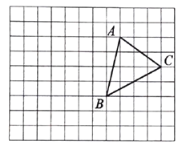
【题目】在如图所示的方格纸中,小正方形的顶点叫做格点,![]() 是一个格点三角形(即
是一个格点三角形(即![]() 的三个顶点都在格点上),根据要求回答下列问题:
的三个顶点都在格点上),根据要求回答下列问题:
![]() 画出
画出![]() 先向左平移6格,再向上平移
先向左平移6格,再向上平移![]() 格所得的
格所得的![]() ;
;
![]() 利用网格画出
利用网格画出![]() 中
中![]() 边上的高
边上的高![]() .
.
![]() 过点
过点![]() 画直线,将
画直线,将![]() 分成面积相等的两个三角形;
分成面积相等的两个三角形;
![]() 画出与
画出与![]() 有一条公共边,且与
有一条公共边,且与![]() 全等的格点三角形.
全等的格点三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点.
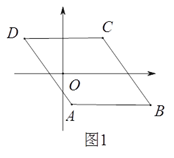
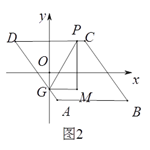
(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com