
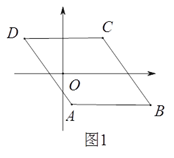
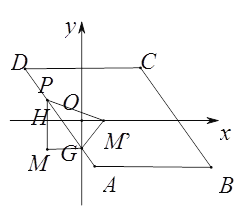
【题目】如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点.
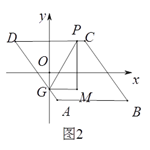
(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
【答案】(1)点P的坐标为(3,4).(2)点P的坐标为(-3,4)或(-1,0)或(5,-4)或(3,-4).(3)点P的坐标为(2,-4)或(![]() ,3)或(
,3)或(![]() ,4)或(
,4)或(![]() ,4).
,4).
【解析】试题(1)点P在BC上,要使PD=CD,只有P与C重合;
(2)首先要分点P在边AB,AD上时讨论,根据“点P关于坐标轴对称的点Q”,即还要细分“点P关于x轴的对称点Q和点P关于y轴的对称点Q”讨论,根据关于x轴、y轴对称点的特征(关于x轴对称时,点的横坐标不变,纵坐标变成相反数;关于y轴对称时,相反;)将得到的点Q的坐标代入直线y=x-1,即可解答;
(3)在不同边上,根据图象,点M翻折后,点M’落在x轴还是y轴,可运用相似求解.
试题解析:解:(1)∵CD=6,∴点P与点C重合,∴点P的坐标是(3,4).
(2)①当点P在边AD上时,由已知得,直线AD的函数表达式为:![]() ,设P(a,-2a-2),且-3≤a≤1.
,设P(a,-2a-2),且-3≤a≤1.
若点P关于x轴对称点Q1(a,2a+2)在直线y=x-1上,∴2a+2=a-1,解得a=-3,此时P(-3,4).
若点P关于y轴对称点Q2(-a,-2a-2)在直线y=x-1上,∴-2a-2=-a-1,解得a=-1,此时P(-1,0).
②当点P在边AB上时,设P(a,-4),且1≤a≤7.
若点P关于x轴对称点Q3(a,4)在直线y=x-1上,∴4=a-1,解得a=5,此时P(5,-4).
若点P关于y轴对称点Q4(-a,-4)在直线y=x-1上,∴-4=-a-1,解得a=3,此时P(3,-4).
综上所述,点P的坐标为(-3,4)或(-1,0)或(5,-4)或(3,-4).
(3)因为直线AD为y=-2x-2,所以G(0,-2).
①如图,当点P在CD边上时,可设P(m,4),且-3≤m≤3,则可得M′P=PM=4+2=6,M′G=GM=|m|,易证得△OGM′∽△HM′P,则![]() ,即
,即![]() ,则OM′=
,则OM′=![]() ,在Rt△OGM′中,由勾股定理得,
,在Rt△OGM′中,由勾股定理得,![]() ,解得m=-
,解得m=-![]() 或
或 ![]() ,则P( -
,则P( -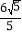 ,4)或(
,4)或( ![]() ,4);
,4);
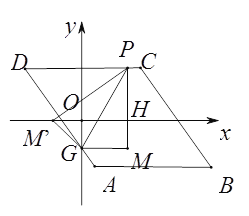
②如下图,当点P在AD边上时,设P(m,-2m-2),则PM′=PM=|-2m|,GM′=MG=|m|,易证得△OGM′∽△HM′P,则![]() ,即
,即![]() ,则OM′=
,则OM′=![]() ,在Rt△OGM′中,由勾股定理得,
,在Rt△OGM′中,由勾股定理得,![]() ,整理得m= -
,整理得m= -![]() ,则P(-
,则P(-![]() ,3);
,3);
如下图,当点P在AB边上时,设P(m,-4),此时M′在y轴上,则四边形PM′GM是正方形,所以GM=PM=4-2=2,则P(2,-4).

综上所述,点P的坐标为(2,-4)或(-![]() ,3)或(-
,3)或(-![]() ,4)或(
,4)或(![]() ,4).
,4).


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某电视台为了解本地区电视节目的收视情况,对部分市民开展了“你最喜爱的电视节目”的问卷调查(每人只填写一项),根据收集的数据绘制了两幅不完整的统计图(如图所示),根据要求回答下列问题:
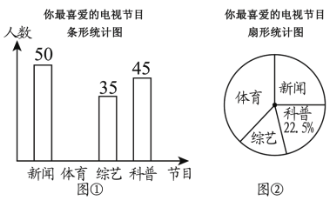
(1)本次问卷调查共调查了________名观众;图②中最喜爱“新闻节目”的人数占调查总人数的百分比为________;
(2)补全图①中的条形统计图;
(3)现有最喜爱“新闻节目”(记为![]() ),“体育节目”(记为
),“体育节目”(记为![]() ),“综艺节目”(记为
),“综艺节目”(记为![]() ),“科普节目”(记为
),“科普节目”(记为![]() )的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“
)的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“![]() ”和“
”和“![]() ”两位观众的概率.
”两位观众的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
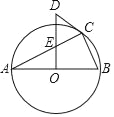
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,∠D=2∠A.
(1)求证:CD是⊙O的切线;
(2)求证:DE=DC;
(3)若OD=5,CD=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈尔滨地铁建设过程中,甲乙两个公司一起竞标了一项工程,甲公司队单独做要用![]() 天,乙公司单独做要用
天,乙公司单独做要用![]() 天;
天;
(1)如果甲乙同时获批合作完成,需要多少天完成?
(2)在施工过程中,监管部门要派一名监督员现场考察,每天补助![]() 元.甲公司每天佣费用为
元.甲公司每天佣费用为![]() 万元;为了赶工期,最终由甲乙两公司合作完成,但要求合作完成该项目的总费用与甲公司单独完成该项目的总费用相同,求平均每天需要支付给乙公司的费用为多少万元?
万元;为了赶工期,最终由甲乙两公司合作完成,但要求合作完成该项目的总费用与甲公司单独完成该项目的总费用相同,求平均每天需要支付给乙公司的费用为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了尽快的适应中招体考项目,现某校初二(1)班班委会准备筹集1800元购买A、B两种类型跳绳供班级集体使用.
(1)班委会决定,购买A种跳绳的资金不少于B种跳绳资金的2倍,问最多用多少资金购买B种跳绳?
(2)经初步统计,初二(1)班有25人自愿参与购买,那么平均每生需交72元.初三(1)班了解情况后,把体考后闲置的跳绳赠送了若干给初二(1)班,这样只需班级共筹集1350元.经初二(1)班班委会进一步宣传,自愿参与购买的学生在25人的基础上增加了4a%.则每生平均交费在72元基础上减少了2.5a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
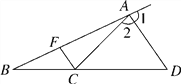
【题目】如图,已知∠1=∠2,∠BAC=20°,∠ACF=80°.
(1)求∠2的度数;
(2)FC与AD平行吗?为什么?
(3)根据以上结论,你能确定∠ADB与∠FCB的大小关系吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,点
中,点![]() 是线段
是线段![]() 上一动点,
上一动点, ![]() 为
为![]() 的中点,
的中点, ![]() 的延长线交BC于
的延长线交BC于![]() .
.
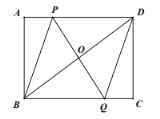
(1)求证: ![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 从点
从点![]() 出发,以l
出发,以l![]() 的速度向
的速度向![]() 运动(不与
运动(不与![]() 重合).设点
重合).设点![]() 运动时间为
运动时间为![]() ,请用
,请用![]() 表示
表示![]() 的长;并求
的长;并求![]() 为何值时,四边形
为何值时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
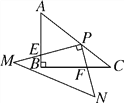
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4.Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种商品按销售量分三部分制定销售单价,如下表:
销售量 | 单价 |
不超过100件的部分 | 2.8元/件 |
超过100件不超过300件的部分 | 2.2元/件 |
超过300件的部分 | 2元/件 |
(1)若买100件花 元,买300件花 元;买380件花 元;
(2)小明买这种商品花了500元,求购买了这种商品多少件;
(3)若小明花了n元(n>280),恰好购买0.4n件这种商品,求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com