
【题目】一种商品按销售量分三部分制定销售单价,如下表:
销售量 | 单价 |
不超过100件的部分 | 2.8元/件 |
超过100件不超过300件的部分 | 2.2元/件 |
超过300件的部分 | 2元/件 |
(1)若买100件花 元,买300件花 元;买380件花 元;
(2)小明买这种商品花了500元,求购买了这种商品多少件;
(3)若小明花了n元(n>280),恰好购买0.4n件这种商品,求n的值.
【答案】(1) 280,720,880;(2) 小明购买这种商品200件;(3) n的值为500
【解析】
(1)由销售量与销售单价计算即可;
(2)设小明购买这种商品x件,由![]() ,得出小明购买的件数大于100件,不足300件,列方程解方程即可;
,得出小明购买的件数大于100件,不足300件,列方程解方程即可;
(3)分两种情况讨论①当280<n≤720时,②当n>720时,分别列方程求解即可.
(1)买100件花:2.8×100=280(元),
买300件花:2.8×100+2.2×(300-100)=720(元),
买380件花:2.8×100+2.2×(300-100)+2×(380-300)=880(元),
故答案为:280,720,880;
(2)设小明购买这种商品x件,
∵![]() ,
,
∴小明购买的件数大于100件,不足300件,
∴![]() ,
,
解得:![]() ;
;
答:小明购买这种商品200件;
(3)∵小明花了n元(n>280),
∴小明购买的件数大于100件,
①当280<n≤720时,
![]() ,
,
解得:![]() ,
,
②当n>720时,
![]() ,
,
解得:n=600(不符合题意,舍去),
综上所述:n的值为500.


科目:初中数学 来源: 题型:
【题目】如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点.
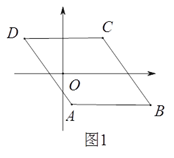
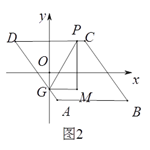
(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:
观察下面由※组成的图案和算式,填空(直接写出答案):

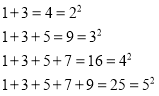
(1)请猜想1+3+5+7+9+11= ;
(2)请猜想1+3+5+7+9+……+(2n-1)= ;
(3)请用上述规律计算:41+43+45+……+97+99= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某企业安排名![]() 工人生产甲、乙两种产品,每人每天生产
工人生产甲、乙两种产品,每人每天生产![]() 件甲产品或
件甲产品或![]() 件乙产品,根据市场需求和生产经验,甲产品每件可获利
件乙产品,根据市场需求和生产经验,甲产品每件可获利![]() 元,乙产品每件可获利
元,乙产品每件可获利![]() 元,而实际生产中,生产乙产品需要额外支出一定的费用,经过核算,每生产
元,而实际生产中,生产乙产品需要额外支出一定的费用,经过核算,每生产![]() 件乙产品,当天平均每件获利减少
件乙产品,当天平均每件获利减少![]() 元,设每天安排
元,设每天安排![]() 人生产乙产品.
人生产乙产品.
![]() 根据信息填表:
根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 |
|
| |
乙 |
|
|
![]() 若每天生产甲产品可获得的利润比生产乙产品可获得的利润多
若每天生产甲产品可获得的利润比生产乙产品可获得的利润多![]() 元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是等边三角形,
是等边三角形,![]() 是等腰直角三角形,∠BAD=90°,AE⊥BD于点E.连CD分别交AE,AB于点F,G,过点A做AH⊥CD交BD于点H,则下列结论:①∠ADC=15°;②AF=AG;③AH=DF;④△ADF≌△BAH;⑤DF=2EH.其中正确结论的个数为( )
是等腰直角三角形,∠BAD=90°,AE⊥BD于点E.连CD分别交AE,AB于点F,G,过点A做AH⊥CD交BD于点H,则下列结论:①∠ADC=15°;②AF=AG;③AH=DF;④△ADF≌△BAH;⑤DF=2EH.其中正确结论的个数为( )
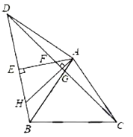
A. 5B. 4C. 3D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
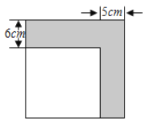
【题目】如图某同学将一个正方形纸片剪去一个宽为![]() 的长条后,再从剩下的长方形纸片上剪去一个宽为
的长条后,再从剩下的长方形纸片上剪去一个宽为![]() 的长条.若两次剪下的长条面积正好相等,则每一个长条的面积为( )
的长条.若两次剪下的长条面积正好相等,则每一个长条的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k为常数,k≠1).
(k为常数,k≠1).
(Ⅰ)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(Ⅱ)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(Ⅲ)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1)、B(x2,y2),当y1>y2时,试比较x1与x2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
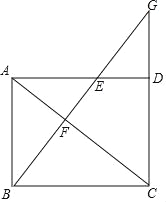
【题目】已知:如图,在平行四边形ABCD中,AC为对角线,E是边AD上一点,BE⊥AC交AC于点F,BE、CD的延长线交于点G,且∠ABE=∠CAD.
(1)求证:四边形ABCD是矩形;
(2)如果AE=EG,求证:AC2=BCBG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com