
【题目】我市某企业安排名![]() 工人生产甲、乙两种产品,每人每天生产
工人生产甲、乙两种产品,每人每天生产![]() 件甲产品或
件甲产品或![]() 件乙产品,根据市场需求和生产经验,甲产品每件可获利
件乙产品,根据市场需求和生产经验,甲产品每件可获利![]() 元,乙产品每件可获利
元,乙产品每件可获利![]() 元,而实际生产中,生产乙产品需要额外支出一定的费用,经过核算,每生产
元,而实际生产中,生产乙产品需要额外支出一定的费用,经过核算,每生产![]() 件乙产品,当天平均每件获利减少
件乙产品,当天平均每件获利减少![]() 元,设每天安排
元,设每天安排![]() 人生产乙产品.
人生产乙产品.
![]() 根据信息填表:
根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 |
|
| |
乙 |
|
|
![]() 若每天生产甲产品可获得的利润比生产乙产品可获得的利润多
若每天生产甲产品可获得的利润比生产乙产品可获得的利润多![]() 元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
【答案】(1)2(65x),1202x;(2)该企业每天生产甲、乙产品可获得总利润是2650元.
【解析】
(1)设每天安排x人生产乙产品,则每天安排(65x)人生产甲产品,每天可生产x件乙产品,每件的利润为(1202x)元,每天可生产2(65x)件甲产品,此问得解;
(2)由总利润=每件产品的利润×生产数量,结合每天生产甲产品可获得的利润比生产乙产品可获得的利润多650元,即可得出关于x的一元二次方程,解之取其较小值得到x值,然后再计算总利润即可.
解:(1)设每天安排x人生产乙产品,则每天安排(65x)人生产甲产品,每天可生产x件乙产品,每件的利润为(1202x)元,每天可生产2(65x)件甲产品.
填表如下:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 |
| 2(65x) |
|
乙 |
|
| 1202x |
(2)依题意,得:15×2(65x)(1202x)x=650,
整理得:x275x+650=0
解得:x1=10,x2=65(不合题意,舍去),
∴15×2(65x)+(1202x)x=2650.
答:该企业每天生产甲、乙产品可获得总利润是2650元.


科目:初中数学 来源: 题型:
【题目】为了尽快的适应中招体考项目,现某校初二(1)班班委会准备筹集1800元购买A、B两种类型跳绳供班级集体使用.
(1)班委会决定,购买A种跳绳的资金不少于B种跳绳资金的2倍,问最多用多少资金购买B种跳绳?
(2)经初步统计,初二(1)班有25人自愿参与购买,那么平均每生需交72元.初三(1)班了解情况后,把体考后闲置的跳绳赠送了若干给初二(1)班,这样只需班级共筹集1350元.经初二(1)班班委会进一步宣传,自愿参与购买的学生在25人的基础上增加了4a%.则每生平均交费在72元基础上减少了2.5a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
甲 | 10 | 6 | 10 | 6 | 8 |
乙 | 7 | 9 | 7 | 8 | 9 |
经过计算,甲进球的平均数为8,方差为3.2.
(1)求乙进球的平均数和方差;
(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB的函数解析式为y=-2x+8,与x轴交于点A,与y轴交于点B。
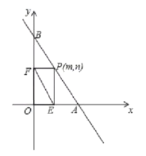
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接E,若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
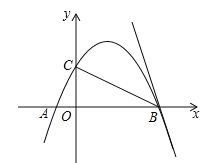
【题目】(2017广东省深圳市)如图,抛物线![]() 经过点A(﹣1,0),B(4,0),交y轴于点C;
经过点A(﹣1,0),B(4,0),交y轴于点C;
(1)求抛物线的解析式(用一般式表示);
(2)点D为y轴右侧抛物线上一点,是否存在点D使![]() ?若存在请直接给出点D坐标;若不存在,请说明理由;
?若存在请直接给出点D坐标;若不存在,请说明理由;
(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种商品按销售量分三部分制定销售单价,如下表:
销售量 | 单价 |
不超过100件的部分 | 2.8元/件 |
超过100件不超过300件的部分 | 2.2元/件 |
超过300件的部分 | 2元/件 |
(1)若买100件花 元,买300件花 元;买380件花 元;
(2)小明买这种商品花了500元,求购买了这种商品多少件;
(3)若小明花了n元(n>280),恰好购买0.4n件这种商品,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校以“我最想去的社会实践地”为课题,开展了一次调查,从全校同学中随机抽取了部分同学进行调查,每位同学从“荪湖花海”、“保国寺”、“慈城古镇”、“绿色学校”中选取一项最想去的社会实践地,并将调查结果绘制成如下的统计图(部分信息未给出).

请根据统计图中信息,解答下列问题:
(1)该调查的样本容量为________,a=________%,b=________%,“荪湖花海”所对应扇形的圆心角度数为________度.
(2)补全条形统计图;
(3)若该校共有1600名学生,请估计全校最想去“绿色学校”的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.
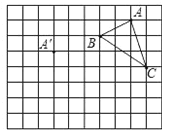
(1)请画出平移后的△A′B′C′,并求△A′B′C′的面积;
(2)若连接AA′,CC′,则这两条线段之间的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,小慧同学利用直尺和规进行了如下操作:①连接AC,分别以点A、C为圆心,以大于![]() AC的长为半径画弧,两弧相交于点P、Q;②作直线PQ,分别交BC、AC、AD于点E、O、F,连接AE、CF.根据操作结果,解答下列问题:
AC的长为半径画弧,两弧相交于点P、Q;②作直线PQ,分别交BC、AC、AD于点E、O、F,连接AE、CF.根据操作结果,解答下列问题:
(1)线段AF与CF的数量关系是 .
(2)若∠BAD=120°,AE平分∠BAD,AB=8,求四边形AECF的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com