
【题目】为了尽快的适应中招体考项目,现某校初二(1)班班委会准备筹集1800元购买A、B两种类型跳绳供班级集体使用.
(1)班委会决定,购买A种跳绳的资金不少于B种跳绳资金的2倍,问最多用多少资金购买B种跳绳?
(2)经初步统计,初二(1)班有25人自愿参与购买,那么平均每生需交72元.初三(1)班了解情况后,把体考后闲置的跳绳赠送了若干给初二(1)班,这样只需班级共筹集1350元.经初二(1)班班委会进一步宣传,自愿参与购买的学生在25人的基础上增加了4a%.则每生平均交费在72元基础上减少了2.5a%,求a的值.
【答案】(1)最多用600元购买B种跳绳;(2)a的值是25.
【解析】
(1)设购买A种跳绳的为x元,则购买B种跳绳的有(1800-x)元,利用“购买A种跳绳的资金不少于B种跳绳资金的2倍”,列出不等式求解即可;
(2)根据“自愿参与购买的学生在25人的基础上增加了4a%,”可得人数为25(1+4a%).根据“每生平均交费在72元基础上减少了2.5a%”可得每生平均交费:72(1-2.5a%),再根据“只需班级共筹集1350元”,列出方程求解即可.
(1)设用于购买A种跳绳的为x元,则购买B种跳绳的有(1800﹣x)元,
根据题意得:2(1800﹣x)≤x,
解得:x≥1200,
∴x取得最小值1200时,1800﹣x取得最大值600,
答:最多用600元购买B种跳绳;
(2)根据题意得:25(1+4a%)×72(1﹣2.5a%)=1350,
令a%=m,
则整理得:40m2﹣6m﹣1=0,
解得:m=![]() 或a=﹣
或a=﹣![]() (舍去),
(舍去),
∴a=25,
所以a的值是25.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】四边形![]() 是正方形,
是正方形,![]() 是直线
是直线![]() 上任意一点,
上任意一点,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .当点G在BC边上时(如图1),易证DF-BE=EF.
.当点G在BC边上时(如图1),易证DF-BE=EF.

(1)当点![]() 在
在![]() 延长线上时,在图2中补全图形,写出
延长线上时,在图2中补全图形,写出![]() 、
、![]() 、
、![]() 的数量关系,并证明;
的数量关系,并证明;
(2)当点![]() 在
在![]() 延长线上时,在图3中补全图形,写出
延长线上时,在图3中补全图形,写出![]() 、
、![]() 、
、![]() 的数量关系,不用证明.
的数量关系,不用证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E为AB边上一点,DE=DC,点F为线段DE上一点,满足∠DFC=∠A,连结CE.
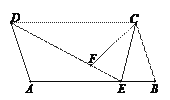
(1)求证:AD=FC;
(2)求证:CE是∠BCF的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某初中对“为贫困家庭捐款活动”进行抽样调查,得到一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8,又知此次调查中捐15元和20元的人数共26人.
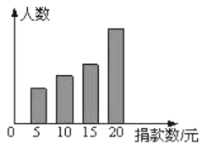
(1)该校一共抽查了________人.
(2)学生捐款数的众数是________元、中位数是________元.
(3)若该校共有1000名学生,请你估算全校学生共捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形②△AED≌△GED③∠DFG=112.5°④BC+FG=1.5其中正确的结论是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知□ABCD,AB//x轴,AB=6,点A的坐标为(1,-4),点D的坐标为(-3,4),点B在第四象限,点P是□ABCD边上的一个动点.
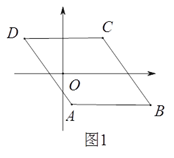
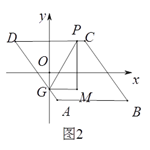
(1)若点P在边BC上,PD=CD,求点P的坐标.
(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.
(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
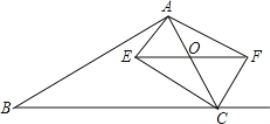
【题目】如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形CEAF是矩形?请证明你的结论。
(3)在第(2)问的结论下,若AE=3,EC=4,AB=12,BC=13,请求出凹四边形ABCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车从甲地到乙地用去油箱中汽油的![]() ,由乙地到丙地用去剩下汽油的
,由乙地到丙地用去剩下汽油的![]() ,油箱中还剩6升汽油.(假设甲地、乙地、丙地、丁地在同一直线上,且按上述顺序分布).
,油箱中还剩6升汽油.(假设甲地、乙地、丙地、丁地在同一直线上,且按上述顺序分布).
(1)求油箱中原有汽油多少升?
(2)若甲、乙两地相距22千米,则乙、丙两地相距多远?(汽车在行驶过程中行驶的路程与耗油量成正比).
(3)在(2)的条件下,若丁地距丙地10千米,问汽车在不加油的情况下,能否去丁地,然后再沿原路返回到甲地?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某企业安排名![]() 工人生产甲、乙两种产品,每人每天生产
工人生产甲、乙两种产品,每人每天生产![]() 件甲产品或
件甲产品或![]() 件乙产品,根据市场需求和生产经验,甲产品每件可获利
件乙产品,根据市场需求和生产经验,甲产品每件可获利![]() 元,乙产品每件可获利
元,乙产品每件可获利![]() 元,而实际生产中,生产乙产品需要额外支出一定的费用,经过核算,每生产
元,而实际生产中,生产乙产品需要额外支出一定的费用,经过核算,每生产![]() 件乙产品,当天平均每件获利减少
件乙产品,当天平均每件获利减少![]() 元,设每天安排
元,设每天安排![]() 人生产乙产品.
人生产乙产品.
![]() 根据信息填表:
根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 |
|
| |
乙 |
|
|
![]() 若每天生产甲产品可获得的利润比生产乙产品可获得的利润多
若每天生产甲产品可获得的利润比生产乙产品可获得的利润多![]() 元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com