
【题目】如图,平行四边形ABCD中,E为AB边上一点,DE=DC,点F为线段DE上一点,满足∠DFC=∠A,连结CE.
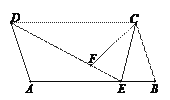
(1)求证:AD=FC;
(2)求证:CE是∠BCF的角平分线.
【答案】(1)见解析;(2)见解析
【解析】(1)由平行四边形性质,及DE=DC,∠DFC=∠A,证△ADE≌△FCD(AAS),得AD=FC.
(2)由△A DE≌△FCD得AE=FD,根据平行四边形性质,再证BE=FE, CF=CB,可再证△CEF≌△CEB(SSS).可得∠FCE=∠BC.
证明:(1)∵四边形ABCD平行四边形,
∴AB∥CD.∴∠AED=∠FDC,
又∵∠A=∠DFC,DE=CD.
∴ △ADE≌△FCD(AAS).
∴AD=FC
(2)∵△A DE≌△FCD
∴AE=FD,
∵BE=AB-AE,EF=DE-DF,
∵四边形ABCD平行四边形,
∴AB=DC,又∵DE=DC,AD=FC,
∴BE=FE, CF=CB,
又∵CE=CE.
∴ △CEF≌△CEB(SSS).
∴∠FCE=∠BCE
∴CE是∠BCF的角平分线.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(1,-4) ,B(3,-3) ,C(1,-1).(每个小方格都是边长为一个单位长度的正方形)
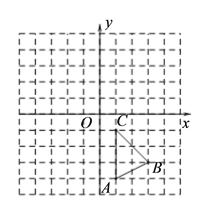
(1)将△ABC沿y轴方向向上平移5个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕点O顺时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点A旋转到点A2所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若点A在数轴上对应的数为![]() ,点B在数轴上对应的数为b,且
,点B在数轴上对应的数为b,且![]() ,b满足
,b满足![]()
(1)求线段AB的长;
![]()
(2)点C在数轴上对应的数为x,且x是方程![]() 的解,在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由;
的解,在数轴上是否存在点P,使得PA+PB=PC?若存在,求出点P对应的数;若不存在,说明理由;
(3)在(1)(2)条件下,点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒4个单位长度和9个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,请问:AB﹣BC的值是否随时间t的变化而改变?若变化,请说明理由;若不变,请求其常数值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x+1)(x-m) (a为常数,a![]() 1)的图像过点(1,2).
1)的图像过点(1,2).
(1)当a=2时,求m的值;
(2)试说明方程a(x+1)(x-m)=0两根之间(不包括两根)存在唯一整数,并求出这个整数;
(3)设M(n,y1)、N(n+1,y2)是抛物线上两点,当n <-1时,试比较y1与y2的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:如图1所示的图形,像我们常见的学习用品——圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:

(1)观察“规形图”,试探究![]() 与
与![]() 之间的关系,并说明理由;
之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在![]() 上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若
上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若![]() ,则
,则![]() ________;
________;
②如图3,DC平分![]() ,EC平分
,EC平分![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
③如图4,![]() 的10 等分线相交于点
的10 等分线相交于点![]() ,若
,若![]() ,求∠A的度数.
,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
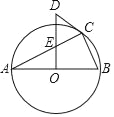
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,∠D=2∠A.
(1)求证:CD是⊙O的切线;
(2)求证:DE=DC;
(3)若OD=5,CD=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A,B在圆上,BC,AD分别与该圆相交于点E,F,G是弧AF的三等分点(弧AG>弧GF),BG交AF于点H.若弧AB的度数为30°,则∠GHF等于( )
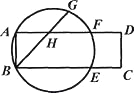
A. 40° B. 45° C. 55° D. 80°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了尽快的适应中招体考项目,现某校初二(1)班班委会准备筹集1800元购买A、B两种类型跳绳供班级集体使用.
(1)班委会决定,购买A种跳绳的资金不少于B种跳绳资金的2倍,问最多用多少资金购买B种跳绳?
(2)经初步统计,初二(1)班有25人自愿参与购买,那么平均每生需交72元.初三(1)班了解情况后,把体考后闲置的跳绳赠送了若干给初二(1)班,这样只需班级共筹集1350元.经初二(1)班班委会进一步宣传,自愿参与购买的学生在25人的基础上增加了4a%.则每生平均交费在72元基础上减少了2.5a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
甲 | 10 | 6 | 10 | 6 | 8 |
乙 | 7 | 9 | 7 | 8 | 9 |
经过计算,甲进球的平均数为8,方差为3.2.
(1)求乙进球的平均数和方差;
(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com