练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，矩形ABCD的顶点A，B在圆上，BC，AD分别与该圆相交于点E，F，G是弧AF的三等分点（弧AG＞弧GF)，BG交AF于点H．若弧AB的度数为30°，则∠GHF等于( )

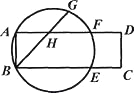
    A. 40° B. 45° C. 55° D. 80°

    【答案】A

    【解析】连接BF，取BF中点O，连接OA、OG，根据90度的圆周角所对的弦是直径可得BF为⊙O的直径，再根据的度数是30°，可知的度数为150°，继而由已知G是的三等分点（)，可得到∠ABG =50°，从而即可得到∠GHF的度数.

    连接BF，取BF中点O，连接OA、OG，

    ∵四边形ABCD是矩形，∴∠BAD=90°，∴BF为⊙O的直径，

    ∵的度数是30°，∴的度数为150°，

    ∵G是的三等分点（)，

    ∴∠FOG=50°，∠AOG=100°，

    ∴∠ABG=∠AOG=50°，

    ∴∠AHB=90°-∠ABG=40°，

    ∴∠GHF=∠AHB=40°，

    故选A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

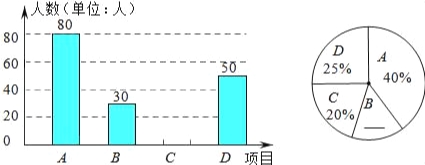
    【题目】某中学开展“阳光体育一小时”活动，根据学校实际情况，决定开设A：踢毽子；B：篮球；C：跳绳；D：乒乓球四种运动项目．为了解学生最喜欢哪一种运动项目，随机抽取了一部分学生进行调查，并将调查结果绘制成如下两个统计图．

    请结合图中的信息解答下列问题：

    （1）本次共调查了多少名学生？

    （2）请将两个统计图补充完整；

    （3）请求出C项目所占的圆心角是 72 度；

    （4）若该中学有1200名学生，喜欢篮球运动项目的学生约有多少名？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知数轴上点A、B、C所表示的数分别是﹣2、+8、x，AC＝6．

    （1）画出数轴并标出点A、B的位置．

    （2）确定x的值为　 　．

    （3）若点M，N分别是AB，AC的中点，求线段MN的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD中，E为AB边上一点，DE＝DC，点F为线段DE上一点，满足∠DFC＝∠A，连结CE．

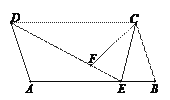
    （1）求证：AD＝FC；

    （2）求证：CE是∠BCF的角平分线．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y＝ax2＋x＋c（a≠0）与x轴交于点A，B两点，

    其中A(－1，0)，与y轴交于点C(0，2)．

    （1）求抛物线的表达式及点B坐标；

    （2）点E是线段BC上的任意一点（点E与B、C不重合），过点E作平行于y轴的直线交抛物线于点F，交x轴于点G．

    ①设点E的横坐标为m，用含有m的代数式表示线段EF的长；

    ②线段EF长的最大值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某初中对“为贫困家庭捐款活动”进行抽样调查，得到一组学生捐款情况的数据.如图是根据这组数据绘制的统计图，图中从左到右各长方形高度之比为3：4：5：8，又知此次调查中捐15元和20元的人数共26人.

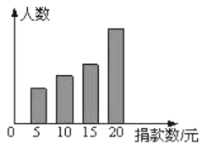
    （1）该校一共抽查了________人.

    （2）学生捐款数的众数是________元、中位数是________元.

    （3）若该校共有1000名学生，请你估算全校学生共捐款多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为1，AC，BD是对角线．将△DCB绕着点D顺时针旋转45°得到△DGH，HG交AB于点E，连接DE交AC于点F，连接FG．则下列结论：

    ①四边形AEGF是菱形②△AED≌△GED③∠DFG=112.5°④BC+FG=1.5其中正确的结论是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

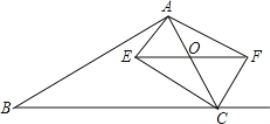
    【题目】如图，在△ABC中，点O是AC边上一动点，过点O作BC的平行线交∠ACB的角平分线于点E，交∠ACB的外角平分线于点F

    (1)求证：EO=FO；

    (2)当点O运动到何处时，四边形CEAF是矩形?请证明你的结论。

    (3)在第(2)问的结论下，若AE=3，EC=4，AB=12，BC=13，请求出凹四边形ABCE的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，射线OA的方向是北偏东20°，射线OB的方向是北偏西40°，OD是OB的反向延长线，OC是∠AOD的平分线。

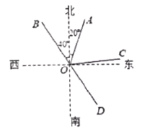
    （1）求∠DOC的度数；

    （2）求出射线OC的方向。

    查看答案和解析>>

    同步练习册答案