
【题目】如图,直线AB的函数解析式为y=-2x+8,与x轴交于点A,与y轴交于点B。
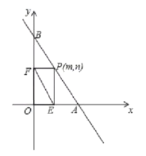
(1)求A、B两点的坐标;
(2)若点P(m,n)为线段AB上的一个动点(与A、B不重合),作PE⊥x轴于点E,PF⊥y轴于点F,连接E,若△PAO的面积为S,求S关于m的函数关系式,并写出m的取值范围。
科目:初中数学 来源: 题型:
【题目】某初中对“为贫困家庭捐款活动”进行抽样调查,得到一组学生捐款情况的数据.如图是根据这组数据绘制的统计图,图中从左到右各长方形高度之比为3:4:5:8,又知此次调查中捐15元和20元的人数共26人.
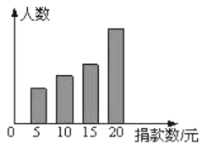
(1)该校一共抽查了________人.
(2)学生捐款数的众数是________元、中位数是________元.
(3)若该校共有1000名学生,请你估算全校学生共捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车从甲地到乙地用去油箱中汽油的![]() ,由乙地到丙地用去剩下汽油的
,由乙地到丙地用去剩下汽油的![]() ,油箱中还剩6升汽油.(假设甲地、乙地、丙地、丁地在同一直线上,且按上述顺序分布).
,油箱中还剩6升汽油.(假设甲地、乙地、丙地、丁地在同一直线上,且按上述顺序分布).
(1)求油箱中原有汽油多少升?
(2)若甲、乙两地相距22千米,则乙、丙两地相距多远?(汽车在行驶过程中行驶的路程与耗油量成正比).
(3)在(2)的条件下,若丁地距丙地10千米,问汽车在不加油的情况下,能否去丁地,然后再沿原路返回到甲地?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线,OC是∠AOD的平分线。
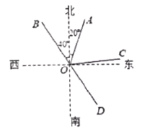
(1)求∠DOC的度数;
(2)求出射线OC的方向。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索规律:
观察下面由※组成的图案和算式,填空(直接写出答案):

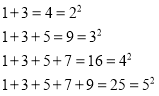
(1)请猜想1+3+5+7+9+11= ;
(2)请猜想1+3+5+7+9+……+(2n-1)= ;
(3)请用上述规律计算:41+43+45+……+97+99= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某企业安排名![]() 工人生产甲、乙两种产品,每人每天生产
工人生产甲、乙两种产品,每人每天生产![]() 件甲产品或
件甲产品或![]() 件乙产品,根据市场需求和生产经验,甲产品每件可获利
件乙产品,根据市场需求和生产经验,甲产品每件可获利![]() 元,乙产品每件可获利
元,乙产品每件可获利![]() 元,而实际生产中,生产乙产品需要额外支出一定的费用,经过核算,每生产
元,而实际生产中,生产乙产品需要额外支出一定的费用,经过核算,每生产![]() 件乙产品,当天平均每件获利减少
件乙产品,当天平均每件获利减少![]() 元,设每天安排
元,设每天安排![]() 人生产乙产品.
人生产乙产品.
![]() 根据信息填表:
根据信息填表:
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 |
|
| |
乙 |
|
|
![]() 若每天生产甲产品可获得的利润比生产乙产品可获得的利润多
若每天生产甲产品可获得的利润比生产乙产品可获得的利润多![]() 元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
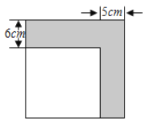
【题目】如图某同学将一个正方形纸片剪去一个宽为![]() 的长条后,再从剩下的长方形纸片上剪去一个宽为
的长条后,再从剩下的长方形纸片上剪去一个宽为![]() 的长条.若两次剪下的长条面积正好相等,则每一个长条的面积为( )
的长条.若两次剪下的长条面积正好相等,则每一个长条的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元?
(2)根据消费者需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的![]() ,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
,已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案?
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数关系式,并说明当m为何值时所获利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com