
����Ŀ��ij�������ۼס���������ë����֪������ë��ÿͲ���ۼ۱�������ë���15Ԫ������ʦ�Ӹ����깺����2Ͳ������ë���3Ͳ������ë������255Ԫ��
��1��������ס���������ë��ÿͲ���ۼ۸��Ƕ���Ԫ��
��2������������������������ò�����8780Ԫ�����ס���������ë��200Ͳ���Ҽ�����ë�����������������ë��������![]() ����֪������ë��ÿͲ�Ľ���Ϊ50Ԫ��������ë��ÿͲ�Ľ���Ϊ40Ԫ��
����֪������ë��ÿͲ�Ľ���Ϊ50Ԫ��������ë��ÿͲ�Ľ���Ϊ40Ԫ��
�����蹺��������ë��mͲ������������ļ��ֽ���������
������������ë�����ȫ���۳��������������������W��Ԫ���������ë�������m��Ͳ��֮��ĺ�����ϵʽ����˵����mΪ��ֵʱ�������������������Ƕ��٣�
���𰸡���1�������������ë��ÿͲ���ۼ�Ϊ60Ԫ��������ë��ÿͲ���ۼ�Ϊ45Ԫ����2���ٽ���������3�֣�������������ڵ�m=78ʱ��������������������Ϊ1390Ԫ��
����������1���������ë��ÿͲ���ۼ�ΪxԪ��������ë��ÿͲ���ۼ�ΪyԪ�����������з����飬�����ô𰸣�
��2�����蹺��������ë��mͲ����������ë��Ϊ��200��m��Ͳ���������ɵõ�����m�IJ���ʽ�飬������m��ȡֵ��Χ����mΪ������������m��ֵ��������ý���������
����m�ɱ�ʾ��W���ɵõ�����m��һ�κ���������һ�κ��������ʿ���ô𰸣�
��1���������ë��ÿͲ���ۼ�ΪxԪ��������ë��ÿͲ���ۼ�ΪyԪ��
��������ɵ�![]() �����
�����![]() ��
��
�𣺸����������ë��ÿͲ���ۼ�Ϊ60Ԫ��������ë��ÿͲ���ۼ�Ϊ45Ԫ��
��2����������������ë��mͲ����������ë��Ϊ��200��m��Ͳ��
��������ɵ�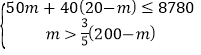 �����75��m��78��
�����75��m��78��
��m������
��m��ֵΪ76��77��78��
�����������3�֣��ֱ�Ϊ��
����һ������������ë��76Ͳ��������ë��Ϊ124Ͳ��
������������������ë��77Ͳ��������ë��Ϊ123Ͳ��
����һ������������ë��78Ͳ��������ë��Ϊ122Ͳ��
�ڸ�������ɵ�W=��60��50��m+��45��40����200��m��=5m+1000��
��5��0��
��W��m�������������75��m��78��
�൱m=78ʱ��W���W���ֵΪ1390��
�𣺵�m=78ʱ��������������������Ϊ1390Ԫ��


 ��һ������ĩ�ٷֳ�̾�ϵ�д�
��һ������ĩ�ٷֳ�̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A����Ϊ(6��0)����B��y����������ϣ���![]() =240.
=240.
(1)���B���ꣻ
(2)����P��B������y�Ḻ���᷽���˶����ٶ�ÿ��2����λ���˶�ʱ��t�룬��AOP�����ΪS����S��t�Ĺ�ϵʽ����ֱ��д��t��ȡֵ��Χ��
(3)��(2)�������£���S��AOP��S��ABP=1:3����S��AOP+S��ABP=S��AOB�����߶�AB�Ĵ�ֱƽ�������Ƿ���ڵ�Q��ʹ�á�AOQ��������BPQ�������ȣ������ڣ����Q�����ꣻ�������ڣ���˵�����ɡ�



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��0����ͬһֱ������ϵ�У�����y=ax��y=ax2��ͼ���п����ǣ�������
A. 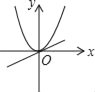 B.
B. 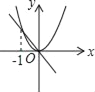 C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
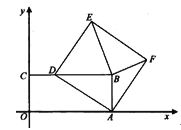
����Ŀ����ͼ����ƽ��ֱ������ϵxoy�У�����OABC�Ķ���B����Ϊ��12,5)����D�� CB���ϴӵ�C�˶�����B����ADΪ����������ADEF����BE��BF���ڵ�D�˶������У���̽���������⣺
(1)��ABF������Ƿ�ı䣬������䣬����ö�ֵ������ı䣬��˵�����ɣ�
(2)����BEFΪ���������Σ����ʱ������ADEF�ı߳���
(3)��E(x,y)��ֱ��д��y����x�ĺ�����ϵʽ���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ƴ˷������ǰ������ɸ���ͬ�IJ�Ϊ����������ij��������������������2��2��2������3��������3��������3��������3���ȣ�����2��2��2����2����������2��Ȧ3�η���������3��������3��������3��������3����������3��������������3��Ȧ4�η�����
��1��ֱ��д�������2������ ��������3�������� ������![]() �������� ����
�������� ����
��2�����㣺24��23+����8����2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���»��̳�����ij�ֱ��䣬ÿ̨������Ϊ2500Ԫ���г����б����������ۼ�Ϊ2900Ԫʱ��ƽ��ÿ�����۳�8̨���������ۼ�ÿ����50Ԫʱ��ƽ��ÿ����ܶ��۳�4̨���̳�Ҫ��ʹ���ֱ������������ƽ��ÿ��ﵽ5000Ԫ����ÿ̨����Ķ���ΪxԪ����x����Ĺ�ϵʽΪ�� ��
A. (x2500)(8+4��![]() )=5000 B. (2900x2500)(8+4��
)=5000 B. (2900x2500)(8+4��![]() )=5000
)=5000
C. (x2500)(8+4��![]() )=5000 D. (2900x)(8+4��
)=5000 D. (2900x)(8+4��![]() )=5000
)=5000
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Щ����£�����Ҫ��������Ҳ�ܰѾ���ֵ����ȥ�������磺|6+7|��6+7��|6��7|��7��6��|7��6|��7��6��|��6��7|��6+7
��1����������Ĺ��ɣ������и�ʽд��ȥ������ֵ���ŵ���ʽ��
��|7��21|���� ������|��![]() ��0.8|���� ������|
��0.8|���� ������|![]() ��
��![]() |���� ����
|���� ����
��2����a�������ϵ�λ����ͼ��ʾ����|a��2.5|���� ����
![]()
A��a��2.5
B.2.5��a
C��a+2.5
D����a��2.5
��3�������������ܵķ��������
��|![]() ��
��![]() |+|
|+|![]() ��
��![]() |��|��
|��|��![]() |+
|+![]() ��
��
��|![]() ��
��![]() |+|
|+|![]() ��
��![]() |��|��
|��|��![]() |+2��
|+2��![]() ��������a��2��
��������a��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
��![]() ��
��![]() .��
.��![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣬����
���е㣬����![]() ��
��![]() ��EF����
��EF����![]() ���ܳ�Ϊ
���ܳ�Ϊ

A. 9B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ൺ���˼��ų��˾����ʦ��ij�������Ӫ��ȫ���ڶ�������ļ���·�Ͻ��еģ�����涨��Ϊ��������Ϊ���������������г����![]() ��λ��ǧ��
��λ��ǧ��![]() ���£�
���£�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()
��1����ʦ���������Ŀ�ĵ�ʱ�����������ʱ�ij������ĸ���������������ض�Զ��
��2����ʦ���������繲�г�����ǧ�ף�
��3����ÿǧ����![]() ��������������ʦ�����˶������ͣ�
��������������ʦ�����˶������ͣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com