练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】类似乘方，我们把求若干个相同的不为零的有理数的除法运算叫做“除方”如2÷2÷2，（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）等，并将2÷2÷2记作2③，读作“2的圈3次方”；（﹣3）÷（﹣3）÷（﹣3）÷（﹣3）记作（﹣3）④，读作“﹣3的圈4次方”．

    （1）直接写出结果：2③＝　 　，（﹣3）④＝　 　，（）⑤＝　 　，

    （2）计算：24÷23+（﹣8）×2③

    【答案】（1），，﹣8；（2）－1

    【解析】

    （1）原式利用题中的新定义计算即可求出值；

    （2）原式利用题中的新定义，以及有理数乘除加减法则计算即可求出值．

    解：（1）根据题中的新定义得：2③＝，（﹣3）④＝，（）⑤＝﹣8；

    故答案为：；；﹣8；

    （2）根据题中的新定义得：原式＝24÷8﹣8×＝3﹣4＝﹣1．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在等边中，点在上，点在的延长线上，且.试探索以下问题：

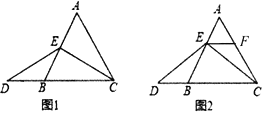
    (1)当点为的中点时，如图1，求证：.

    (2)如图2，当点不是的中点时，过点作，交于点，求证：是等边三角形.

    (3)在(2)的条件下，与还相等吗？请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】滴滴公布了新的滴滴快车计价规则，车费由“总里程费+总时长费”两部分构成，不同时段收费标准不同，具体收费标准如下表，如果车费不足起步价，则按起步价收费.

    时间段

    里程费（元/千米）

    时长费（元/分钟）

    起步价（元）

    06:00-10:00

    1.80

    0.80

    14.00

    10:00-17:00

    1.45

    0.40

    13.00

    17:00-21:00

    1.50

    0.80

    14.00

    21:00-6:00

    0.80

    0.80

    14.00

    （1）小明早上7:10乘坐滴滴快车上学，行车里程6千米，行车时间10分钟，则应付车费多少元？

    （2）小云17:10放学回家，行车里程2千米，行车时间12分钟，则应付车费多少元？

    （3）下晚自习后小明乘坐滴滴快车回家，20:45在学校上车，由于堵车，平均速度是千米/小时，15分钟后走另外一条路回家，平均速度是千米/小时，10分钟后到家，则他应付车费多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将边长OA=8，OC=10的矩形OABC放在平面直角坐标系中，顶点O为原点，顶点C、A分别在轴和y轴上.在OA边上选取适当的点E，连接CE，将△EOC沿CE折叠。

    （1）如图①，当点O落在AB边上的点D处时，点E的坐标为 ；

    （2）如图②，当点O落在矩形OABC内部的点D处时，过点E作EG∥轴交CD于点H，交BC于点G.求证：EH＝CH；

    （3）在（2）的条件下，设H（m，n），写出m与n之间的关系式 ；

    （4）如图③，将矩形OABC变为正方形，OC＝10，当点E为AO中点时，点O落在正方形OABC内部的点D处，延长CD交AB于点T，求此时AT的长度。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：

    （1）23﹣6×（﹣3）+2×（﹣4）；

    （2）﹣1.53×0.75﹣0.53×（）；

    （3）﹣14+|3﹣5|﹣16÷（﹣2）×

    （4）﹣14+×[2×（﹣6）﹣（﹣4）2]．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某网店销售甲、乙两种羽毛球，已知甲种羽毛球每筒的售价比乙种羽毛球多15元，王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球，共花费255元．

    （1）该网店甲、乙两种羽毛球每筒的售价各是多少元？

    （2）根据消费者需求，该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒，且甲种羽毛球的数量大于乙种羽毛球数量的，已知甲种羽毛球每筒的进价为50元，乙种羽毛球每筒的进价为40元．

    ①若设购进甲种羽毛球m筒，则该网店有哪几种进货方案？

    ②若所购进羽毛球均可全部售出，请求出网店所获利润W（元）与甲种羽毛球进货量m（筒）之间的函数关系式，并说明当m为何值时所获利润最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】同学报名次参加学校秋季运动会，有以下5个项目可供选择：径赛项目：100m、200m、1000m（分别用A1、A2、A3表示）；田赛项目：跳远，跳高（分别用T1、T2表示）

    （1）该同学从5个项目中任选一个，恰好是田赛项目的概率P为___________；

    （2）该同学从5个项目中任选两个，求恰好是一个径赛项目和一个田赛项目的概率P1，利用列表法或树状图加以说明；

    （3）该同学从5个项目中任选两个，则两个项目都是径赛项目的概率P2为___________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(12分)如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB于点D.点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．

    (1)求线段CD的长；

    (2)设△CPQ的面积为S，求S与t之间的函数关系式，并确定在运动过程中是否存在某一时刻t，使得S△CPQ∶S△ABC＝9∶100？若存在，求出t的值；若不存在，说明理由；

    (3)当t为何值时，△CPQ为等腰三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点为轴负半轴上一点，点为轴正半轴上一点，、的长分别是关于的一元二次方程的两根，，且，则的度数为________.

    查看答案和解析>>

    同步练习册答案