
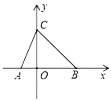
【题目】如图,点![]() 为
为![]() 轴负半轴上一点,点
轴负半轴上一点,点![]() 为
为![]() 轴正半轴上一点,
轴正半轴上一点,![]() 、
、![]() 的长分别是关于
的长分别是关于![]() 的一元二次方程
的一元二次方程![]() 的两根,
的两根,![]() ,且
,且![]() ,则
,则![]() 的度数为________.
的度数为________.
 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
【题目】类似乘方,我们把求若干个相同的不为零的有理数的除法运算叫做“除方”如2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等,并将2÷2÷2记作2③,读作“2的圈3次方”;(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作“﹣3的圈4次方”.
(1)直接写出结果:2③= ,(﹣3)④= ,(![]() )⑤= ,
)⑤= ,
(2)计算:24÷23+(﹣8)×2③
查看答案和解析>>
科目:初中数学 来源: 题型:
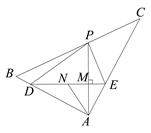
【题目】△ABC中,AB=6,AC=8,BC=10,P为BC边上一动点,过线段AP上的点M作DE⊥AP,交边AB于点D,交边AC于点E,点N为DE中点,若四边形ADPE的面积为18,则AN的最大值=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
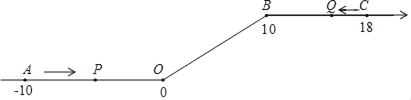
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位,动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半;点P从点A出发的同时,点Q从点C出发,以1单位/秒的速度沿着“折线数轴”的负方向运动,当点P到达B点时,点P、Q均停止运动.设运动的时间为t秒.问:
(1)用含t的代数式表示动点P在运动过程中距O点的距离;
(2)P、Q两点相遇时,求出相遇时间及相遇点M所对应的数是多少?
(3)是否存在P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等时?若存在,请直接写出t的取值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,点
两点,点![]() 是
是![]() 轴上一动点,要使点
轴上一动点,要使点![]() 关于直线
关于直线![]() 的对称点刚好落在
的对称点刚好落在![]() 轴上,则此时点
轴上,则此时点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青岛交运集团出租车司机张师傅某天下午的营运全是在东西走向的吉林路上进行的,如果规定向东为正,向西为负,他这天下午行车里程![]() 单位:千米
单位:千米![]() 如下:
如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)张师傅这天最后到达目的地时,在下午出车时的出发地哪个方向?距离出发地多远?
(2)张师傅这天下午共行车多少千米?
(3)若每千米耗油![]() ,则这天下午张师傅用了多少升油?
,则这天下午张师傅用了多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB:y=kx+4(k≠0)与x轴,y轴,交于A、B两点,点C是BO的中点且tan∠ABO=![]()
(1)求直线AC的解析式;
(2)若点M是直线AC的一点,当![]() 时,求点M的坐标.
时,求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知ab<0,![]() ,且|c|>|b|>|a|,数轴上a、b、c对应的点是A、B、C.
,且|c|>|b|>|a|,数轴上a、b、c对应的点是A、B、C.
(1) 若|a|=-a时,请在数轴上标出A、B、C的大致位置;
(2) 在(1)的条件下,化简:|a-b|-|b+c|+|c+a|.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料
小白遇到这样一个问题:
如图,点C是段AB的中点,AD=![]() DB,CD=10,求AB的长.
DB,CD=10,求AB的长.
![]()
小白的思路是:设AB=x,根据“CD=10“列方程,请按照小白的思路完成此问题的解答
用学过的知识或参考小白的方法,解决下面的问题:
已知OC、OD是∠AOB的内部的两条射线,∠AOC═![]() ∠AOB,∠AOD=m∠DOB,∠COD=n(m、n为常数,且m≠
∠AOB,∠AOD=m∠DOB,∠COD=n(m、n为常数,且m≠![]() )
)
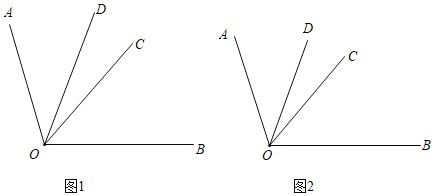
(1)如图1,若m=![]() ,n=22,求∠DOB的度数.
,n=22,求∠DOB的度数.
(2)如图2,若n=14(3﹣2m)求∠DOB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com