
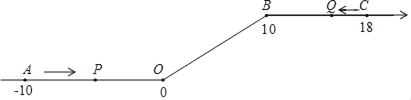
����Ŀ����ͼ����һ��������ԭ��O�͵�B������һ�£��õ�һ�����������ᡱ��ͼ�е�A��ʾ��10����B��ʾ10����C��ʾ18�����dzƵ�A�͵�C�����������28�����ȵ�λ������P�ӵ�A��������2��λ/����ٶ����š��������ᡱ���������˶����ӵ�O�˶�����B�ڼ��ٶȱ�Ϊԭ����һ�룻��P�ӵ�A������ͬʱ����Q�ӵ�C��������1��λ/����ٶ����š��������ᡱ�ĸ������˶�������P����B��ʱ����P��Q��ֹͣ�˶������˶���ʱ��Ϊt�룮�ʣ�
��1���ú�t�Ĵ���ʽ��ʾ����P���˶������о�O��ľ��룻
��2��P��Q��������ʱ���������ʱ�估������M����Ӧ�����Ƕ��٣�
��3���Ƿ����P��O���������������ij�����Q��B���������������ij������ʱ�������ڣ���ֱ��д��t��ȡֵ���������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2������ʱ��Ϊ
����2������ʱ��Ϊ![]() �룬��M����Ӧ������
�룬��M����Ӧ������![]() ����3�����ڣ�t��2��t��
����3�����ڣ�t��2��t��![]() ��
��
��������
��1���ֵ�P��AO�Ϻ͵�P��OB������������������P��ÿ��ʱt��ȡֵ��Χ���ٸ�������ֱ��г�����ʽ�ɵô𰸣�
��2����������ʱP��Q�˶���ʱ����ȣ�P��Q�˶��ľ���͵���28�ɵ÷��̣����ݽⷽ�̣��ɵô𰸣�
��3����0��t��5��5��t��8��8��t��15�������������PO=BQ���ɵ÷��̣��ֱ������̣��ɵô𰸣�
�⣺��1���趯��P���˶������о�O��ľ���ΪS����P��A�˶���Oʱ,����ʱ��Ϊ��![]() ���룩��
���룩��
��0��t��5ʱ��S��10��2t��
��P��O�˶���Bʱ,����ʱ��Ϊ��![]() ���룩
���룩
��P��A�˶���Bʱ,����ʱ��Ϊ��15��
��5��t��15ʱ��S��t��5��
������P���˶������о�O��ľ���S��![]() ��
��
��2���辭��a�룬P��Q�������������P�˶��ľ���Ϊ10+��a-5������Q�˶��ľ���Ϊa,
10+��a-5��+a=28
��ã�a��![]() ��
��
���M����Ӧ�����ǣ�18��![]() ��
��![]() ��
��
����M����Ӧ������![]() ��
��
��3�����ڣ�t��2��t��![]() ��
��
���ɣ���0��t��5ʱ��
10��2t����18��10��t����1��
��ã�t��2
��5��t��8ʱ��
��t��10��2����1����18��10��t����1��
��ã�t��![]() ��
��
��8��t��15ʱ��
��t��10��2����1��[t����18��10����1]��1
�÷����⣬
�ʴ��ڣ�t��2��t��![]() ��
��
�ʴ�Ϊ����1��![]() ����2������ʱ��Ϊ
����2������ʱ��Ϊ![]() �룬��M����Ӧ������
�룬��M����Ӧ������![]() ����3�����ڣ�t��2��t��
����3�����ڣ�t��2��t��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��AB��DF����D+��B=180����

��1����֤��DE��BC��
��2�������AMD=75�������AGC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ı���ABCD�������Σ�G��CD���ϵ�һ�����㣨��G��C��D���غϣ�����CGΪһ����������ABCD����������CEFG������BG��DE������̽������ͼ���߶�BG���߶�DE�ij��ȹ�ϵ������ֱ�ߵ�λ�ù�ϵ��

��1������ͼ1���߶�BG���߶�DE�ij��ȹ�ϵ������ֱ�ߵ�λ�ù�ϵ��
��2����ͼ1�е�������CEFG���ŵ�C��˳ʱ�루����ʱ�룩������ת����Ƕ�a���õ���ͼ2����ͼ3���Σ�����ͨ���۲졢�����ȷ����жϣ�1���еõ��Ľ����Ƿ���Ȼ��������ѡȡͼ2֤������жϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=�� ![]() ��7x+
��7x+ ![]() �����Ա���x�ֱ�ȡx1 �� x2 �� x3 �� �ҩ�13��x1��0��x3��x2��2�����Ӧ�ĺ���ֵy1 �� y2 �� y3�Ĵ�С��ϵ��ȷ���ǣ� ��
�����Ա���x�ֱ�ȡx1 �� x2 �� x3 �� �ҩ�13��x1��0��x3��x2��2�����Ӧ�ĺ���ֵy1 �� y2 �� y3�Ĵ�С��ϵ��ȷ���ǣ� ��
A.y1��y2��y3
B.y1��y2��y3
C.y2��y3��y1
D.��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij��������2015�꿪ʼ���ܼ��ţ����ƶ���������ŷţ���ͼ�ֱ��Ǹó�2015��2018����������ŷ���(��λ����)��������������ͳ��ͼ������ͼ����Ϣ�ش��������⣮
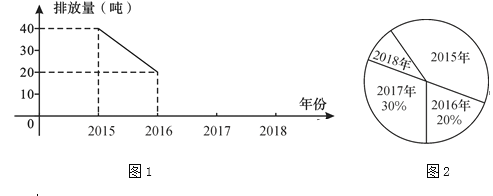
(1)��ó�2015��2018����������ŷ�������
(2)��ͼ������ͳ��ͼ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��֪��AOB��OA=OB����E��OB���ϣ��ı���AEBF�Ǿ��Σ�����ֻ���̶ȵ�ֱ����ͼ�л�������AOBG�����뱣����ͼ�ۼ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����E�ǡ�ABC�����ģ�AE���ӳ��߽�BC�ڵ�F������ABC�����Բ��O�ڵ�D������BD������D��ֱ��DM��ʹ��BDM=��DAC�� ������֤��ֱ��DM�ǡ�O�����ߣ�
������֤��DE2=DFDA��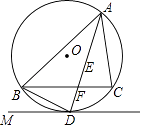
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�κ��ʱ����ѧ�������״�����Բ��������Բ���ʣ�����ʱ����չ��������������Ƶ�ʹ��Ƹ�����һԭ�����������ģ��ķ�����Բ���ʦн��й��ƣ��ü�����������m���������ԣ�x��y����x��y��ʵ������0��x��1��0��y��1�������Ƕ�Ӧ�ĵ���ƽ��ֱ������ϵ��ȫ����ijһ�������εı߽缰���ڲ������ͳ�Ƴ���Щ���е�ԭ��ľ���С�ڻ����1�ĵ���n������ݴ˿ɹ��Ʀе�ֵΪ �� ���ú�m��n��ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90����AC=BC������C����ABC����ֱ��MN��AM��MN��M��BN��MN��N��
��1����֤��MN=AM+BN��

��2��������C����ABC����ֱ��MN��AM��MN��M��BN��MN��N����AM��BN��MN֮����ʲô��ϵ����˵�����ɡ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com