练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图已知∠AOB，OA=OB，点E在OB边上，四边形AEBF是矩形，请你只用无刻度的直尺在图中画出菱形AOBG．（请保留画图痕迹）．

    【答案】解：如图所示：


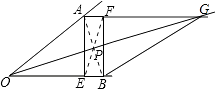
    【解析】由已知OA=OB，想到连接AB，可得等腰△OAB，AB是所要求作的菱形AOBG的一条对角线，就要找到AB的中点，由四边形AEBF是矩形，矩形的对角线互相平分，因此连接EF，设AB和EF相交于点P，可知OP垂直平分线段AB，延长OP使PG=OP，即可作出菱形AOBG。此题作图的依据是对角线互相垂直平分的四边形是菱形。
    【考点精析】解答此题的关键在于理解菱形的判定方法的相关知识，掌握任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形，以及对矩形的性质的理解，了解矩形的四个角都是直角，矩形的对角线相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】声音在空气中传播的速度y(m/s)(简称音速)与气温x(℃)的关系如下表:

    气温x(℃)

    0

    5

    10

    15

    20

    音速y(m/s)

    331

    334

    337

    340

    343

    (1)这一变化过程中，自变量和因变量各是什么?

    (2)音速y(m/s)与气温x(℃)之间的关系式；

    (3)气温x=22℃时，某人看到烟花烯放5s后才听到声音，那么此人与燃烟花的所在地约相距多远?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】目前，我市城市居民用电收费方式有以下两种:

    普通电价付费方式:全天0. 52元/度;

    峰谷电价付费方式:峰时(早8:00~晚21:00)0. 65元/度;谷时(晚21:00~早8:00)0. 40元/度.

    (1)小丽老师家10月份总用电量为280度.

    ①若其中峰时电量为80度，则小丽老师家按照哪种方式付电费比较合适?能省多少元?

    ②若小丽老师交费137元，那么，小丽老师家峰时电量为多少度?

    (2)到11月份付费时，小丽老师发现11月份总用电量为320度，用峰谷电价付费方式比普通电价付费方式省了18. 4元，那么，11月份小丽老师家峰时电量为多少度?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在开展“经典阅读”活动中，某学校为了解全校学生利用课外时间阅读的情况，学校团委随机抽取若干名学生，调查他们一周的课外阅读时间，并根据调查结果绘制了如下尚不完整的统计表．根据图表信息，解答下列问题：

    　　　　频率分布表

    阅读时间(小时)

    频数(人)

    频率

    1≤x＜2

    18

    0.12

    2≤x＜3

    a

    m

    3≤x＜4

    45

    0.3

    4≤x＜5

    36

    n

    5≤x＜6

    21

    0.14

    合计

    b

    1

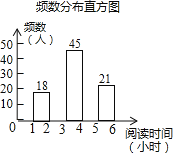
    (1)填空：a＝ ，b＝ ，m＝ ，n＝ ；

    (2)将频数分布直方图补充完整(画图后请标注相应的频数)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

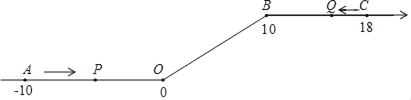
    【题目】如图，将一条数轴在原点O和点B处各折一下，得到一条“折线数轴”．图中点A表示﹣10，点B表示10，点C表示18，我们称点A和点C在数轴上相距28个长度单位，动点P从点A出发，以2单位/秒的速度沿着“折线数轴”的正方向运动，从点O运动到点B期间速度变为原来的一半；点P从点A出发的同时，点Q从点C出发，以1单位/秒的速度沿着“折线数轴”的负方向运动，当点P到达B点时，点P、Q均停止运动．设运动的时间为t秒．问：

    （1）用含t的代数式表示动点P在运动过程中距O点的距离；

    （2）P、Q两点相遇时，求出相遇时间及相遇点M所对应的数是多少？

    （3）是否存在P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等时？若存在，请直接写出t的取值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是权威机构公布的一组反映世界人口的数据：1957年世界人口为30亿，17年后(即1974年)增加了10亿，即达到40亿；又过了13年达到50亿；到1999年全世界人口达到60亿．以此速度，人口学专家预测到2025年，世界人口将达到80亿；而到2050年世界人口将超过90亿，其中亚洲人口最多，将达到52.68亿，北美洲3.92亿，欧洲8.28亿，拉丁美洲及加勒比地区8.09亿，非洲17.68亿．有一位同学根据以上提供的数据制作了三幅统计图，请根据这些统计图回答问题．

    　

    (1)三幅统计图分别表示了什么内容？

    (2)从哪幅统计图中最能看出世界人口的总体变化情况？

    (3)2050年非洲人口大约将达到多少亿？你是从哪幅统计图中得到这个数据的？

    (4)2050年亚洲人口比其他各洲人口的总和还要多，你从哪幅统计图中可以明显地得到这个结论？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列命题中：

    ①长为的线段沿某一方向平移后，平移后线段的长为；

    ②三角形的高在三角形内部；

    ③六边形的内角和是外角和的两倍；

    ④平行于同一直线的两直线平行；

    ⑤两个角的两边分别平行，则这两个角相等，真命题个数有（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

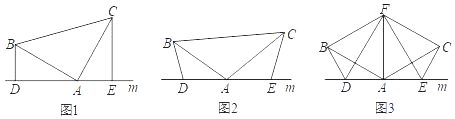
    【题目】（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．证明：DE＝BD+CE．

    （2）如图（2），将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角．请问结论DE＝BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．

    （3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA＝∠AEC＝∠BAC，试判断△DEF的形状并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从邵阳市到长沙的高铁列车里程比普快列车里程缩短了75千米，运行时间减少了4小时，已知邵阳市到长沙的普快列车里程为306千米，高铁列车平均时速是普快列车平均时速的3.5倍．

    (1)求高铁列车的平均时速；

    (2)某日刘老师从邵阳火车南站到长沙市新大新宾馆参加上午11：00召开的会议，如果他买到当日上午9：20从邵阳市火车站到长沙火车南站的高铁票，而且从长沙火车南站到新大新宾馆最多需要20分钟．试问在高铁列车准点到达的情况下他能在开会之前赶到吗？

    查看答案和解析>>

    同步练习册答案