
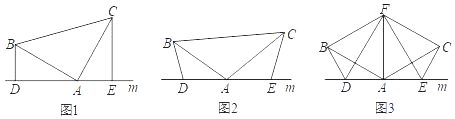
����Ŀ����1����ͼ��1������֪������ABC�У���BAC��90����AB��AC��ֱ��m������A��BD��ֱ��m��CE��ֱ��m������ֱ�Ϊ��D��E��֤����DE��BD+CE��
��2����ͼ��2��������1���е�������Ϊ������ABC�У�AB��AC��D��A��E���㶼��ֱ��m�ϣ������С�BDA����AEC����BAC������������Ϊ������ǻ�۽ǣ����ʽ���DE��BD+CE�Ƿ��������������������֤����������������˵�����ɣ�
��3����չ��Ӧ�ã���ͼ��3����D��E��D��A��E��������ֱ��m�ϵ������㣨D��A��E���㻥���غϣ�����FΪ��BACƽ�����ϵ�һ�㣬����ABF����ACF��Ϊ�ȱ������Σ�����BD��CE������BDA����AEC����BAC�����ж���DEF����״��˵�����ɣ�
���𰸡���1��������. ��2��������. ��3����DEFΪ�ȱ������Σ�������.
��������
��1������BD��ֱ��m��CE��ֱ��m�á�BDA����CEA��90��������BAC��90�������ݵȽǵ������ȵá�CAE����ABD��Ȼ�������AAS�����ж���ADB�ա�CEA����AE��BD��AD��CE������DE��AE+AD��BD+CE��
��2���ɡ�BDA����AEC����BAC��120�����Ϳ��������BAD����ACE��������AAS�Ϳ��Եó���BAD�ա�ACE���Ϳ��Եó�BD��AE��DA��CE�����ɵó����ۣ�
��3���ɵȱ������ε����ʣ����������BAC��120�����Ϳ��Եó���BAD�ա�ACE������BD��AE�������ó���BDF�ա�AEF���ó�DF��EF����BFD����AFE�����ó���DFE��60����������DEFΪ�ȱ������Σ�
��1����ͼ1��

��BD��ֱ��m��CE��ֱ��m��
���BDA����CEA��90����
�ߡ�BAC��90����
���BAD+��CAE��90��
�ߡ�BAD+��ABD��90����
���CAE����ABD��
����ADB����CEA��
 ��
��
���ADB�ա�CEA��AAS����
��AE��BD��AD��CE��
��DE��AE+AD��BD+CE��
��2����ͼ2��

�ߡ�BDA����BAC������
���DBA+��BAD����BAD+��CAE��180��������
���DBA����CAE��
����ADB����CEA��
 ��
��
���ADB�ա�CEA��AAS����
��AE��BD��AD��CE��
��DE��AE+AD��BD+CE��
��3����ͼ3��

�ɣ�2����֪����ADB�ա�CEA��
��BD��AE����DBA����CAE��
�ߡ�ABF����ACF��Ϊ�ȱ������Σ�
���ABF����CAF��60����BF��AF��
���DBA+��ABF����CAE+��CAF��
���DBF����FAE��
������DBF����EAF��
 ��
��
���DBF�ա�EAF��SAS����
��DF��EF����BFD����AFE��
���DFE����DFA+��AFE����DFA+��BFD��60����
���DEFΪ�ȱ������Σ�


 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽƬABCD��AD��AB���У������۵���ʹ��A���C�غϣ��ۺ�EF��AD�ڵ�E����BC�ڵ�F����AC�ڵ�O������AF��CE.
��1����֤���ı���AFCE�����Σ�
��2����AE��8����ABF�����Ϊ9����AB��BF��ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��֪��AOB��OA=OB����E��OB���ϣ��ı���AEBF�Ǿ��Σ�����ֻ���̶ȵ�ֱ����ͼ�л�������AOBG�����뱣����ͼ�ۼ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��y�ķ�����![]() �����У�3��a��1���������н��ۣ�����a=1ʱ��������Ľ�Ҳ�Ƿ���x��y=4��a�Ľ⣻����a=��2ʱ��x��y��ֵ��Ϊ�෴��������x��1����1��y��4����
�����У�3��a��1���������н��ۣ�����a=1ʱ��������Ľ�Ҳ�Ƿ���x��y=4��a�Ľ⣻����a=��2ʱ��x��y��ֵ��Ϊ�෴��������x��1����1��y��4����![]() �Ƿ�����Ľ⣬������ȷ���ǣ� ��
�Ƿ�����Ľ⣬������ȷ���ǣ� ��
A.�٢�B.�ۢ�C.�٢ڢ�D.�٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ�κ��ʱ����ѧ�������״�����Բ��������Բ���ʣ�����ʱ����չ��������������Ƶ�ʹ��Ƹ�����һԭ�����������ģ��ķ�����Բ���ʦн��й��ƣ��ü�����������m���������ԣ�x��y����x��y��ʵ������0��x��1��0��y��1�������Ƕ�Ӧ�ĵ���ƽ��ֱ������ϵ��ȫ����ijһ�������εı߽缰���ڲ������ͳ�Ƴ���Щ���е�ԭ��ľ���С�ڻ����1�ĵ���n������ݴ˿ɹ��Ʀе�ֵΪ �� ���ú�m��n��ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() ��ʾ������
��ʾ������![]() ��������������磺
��������������磺![]() ��
��![]() ��
��![]() ����
����![]() ��ʾ����
��ʾ����![]() ����С���������磺
����С���������磺![]() ��
��![]() ��
��![]() .����������⣺
.����������⣺
��1��![]() = ,��
= ,��![]() = ��
= ��
��2����![]() =2����
=2����![]() ��ȡֵ��Χ�� ����
��ȡֵ��Χ�� ����![]() =��1����
=��1����![]() ��ȡֵ��Χ�� ��
��ȡֵ��Χ�� ��
��3����֪![]() ��
��![]() ���㷽����
���㷽����![]() ����
����![]() ��
��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���x2����2k��1��x+k2=0����������ȵ�ʵ��������ôk���������ֵ�ǣ� ��
A.��2
B.��1
C.0
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������н�����ͼ��ֱ������ϵ����������A��O��B��λ����ͼ�����Ƿֱ��ǣ���1��1������0��0���ͣ�1��0���� 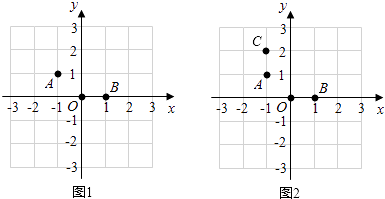
��1����ͼ2����������C��ʹA��O��B��C�Ŀ����ӳ�Ϊһ����Գ�ͼ�Σ�����ͼ�л�����ͼ�εĶԳ��
��2�����������λ������һ������P��ʹA��O��B��P�Ŀ����ӳ�Ϊһ����Գ�ͼ�Σ���ֱ��д������P��λ�õ����꣮��д��2�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ϲ��̽��������ͬѧ�ó���״�ֱ��dz����κ������ε�����ֽƬ�����г�����ֽƬ�ij�Ϊ![]() ����Ϊ
����Ϊ![]() ��������ֽƬ�����ȣ�
��������ֽƬ�����ȣ�
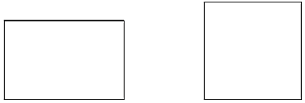
��1��������֪��������ֽƬ�ı߳�������������������ֽƬ�ı߳���������������ţ�
��2���ڳ�����ֽƬ�Ͻس�����������������ֽƬ������ֱ�Ϊ![]() ��
��![]() ��������Ϊ����������ֽƬ�����֮��С�ڳ�����ֽƬ�������������һ���ܽس�����Ҫ���������ֽƬ������ͬ�������ļ�����Ϊʲô�����ο����ݣ�
��������Ϊ����������ֽƬ�����֮��С�ڳ�����ֽƬ�������������һ���ܽس�����Ҫ���������ֽƬ������ͬ�������ļ�����Ϊʲô�����ο����ݣ�![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com