练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列命题中：

    ①长为的线段沿某一方向平移后，平移后线段的长为；

    ②三角形的高在三角形内部；

    ③六边形的内角和是外角和的两倍；

    ④平行于同一直线的两直线平行；

    ⑤两个角的两边分别平行，则这两个角相等，真命题个数有（ ）

    A.B.C.D.

    【答案】A

    【解析】

    利用平移的性质、三角形高的定义、多边形的外角与内角、平行线的性质分别判断出正确答案的个数，即可得出答案.

    ①：平移不改变图形的形状和大小，故选项①错误；

    ②：直角三角形的高在三角形的边上，钝角三角形的高在三角形的外面，故选项②错误；

    ③：六边形的外角和360°，六边形的内角和720°，故选项③正确；

    ④：在同一平面内，平行于同一条直线的两条直线平行，故选项④错误；

    ⑤：两个角的两边分别平行，则这两个角相等或互补，故选项⑤错误.

    因此正确的个数有两个，答案选择A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，E，F分别为边AB，CD的中点，连接DE、BF、BD．

    （1）求证：△ADE≌△CBF．

    （2）若AD⊥BD，则四边形BFDE是什么特殊四边形？请证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=﹣ ﹣7x+ ，若自变量x分别取x1 ， x2 ， x3 ， 且﹣13＜x1＜0，x3＞x2＞2，则对应的函数值y1 ， y2 ， y3的大小关系正确的是（ ）
    A.y1＞y2＞y3
    B.y1＜y2＜y3
    C.y2＞y3＞y1
    D.无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图已知∠AOB，OA=OB，点E在OB边上，四边形AEBF是矩形，请你只用无刻度的直尺在图中画出菱形AOBG．（请保留画图痕迹）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点E是△ABC的内心，AE的延长线交BC于点F，交△ABC的外接圆⊙O于点D，连接BD，过点D作直线DM，使∠BDM=∠DAC． （Ⅰ）求证：直线DM是⊙O的切线；
    （Ⅱ）求证：DE2=DFDA．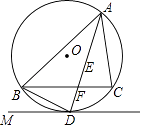

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x，y的方程组，其中－3≤a≤1，给出下列结论：①当a=1时，方程组的解也是方程x＋y=4－a的解；②当a=－2时，x、y的值互为相反数；③若x≤1，则1≤y≤4；④是方程组的解，其中正确的是（ ）

    A.①②B.③④C.①②③D.①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我国魏晋时期数学家刘徽首创“割圆术”计算圆周率．随着时代发展，现在人们依据频率估计概率这一原理，常用随机模拟的方法对圆周率π进行估计，用计算机随机产生m个有序数对（x，y）（x，y是实数，且0≤x≤1，0≤y≤1），它们对应的点在平面直角坐标系中全部在某一个正方形的边界及其内部．如果统计出这些点中到原点的距离小于或等于1的点有n个，则据此可估计π的值为 ． （用含m，n的式子表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的方程x2﹣（2k﹣1）x+k2=0有两个不相等的实数根，那么k的最大整数值是（ ）
    A.﹣2
    B.﹣1
    C.0
    D.1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以直角三角形AOC的直角顶点O为原点，以OC、OA所在直线为x轴和y轴建立平面直角坐标系，点A（0，a），C（b，0）满足．D为线段AC的中点．在平面直角坐标系中，以任意两点P（x1，y1）、Q（x2，y2）为端点的线段中点坐标为，．

    （1）则A点的坐标为　 　；点C的坐标为　 　．D点的坐标为　 　．

    （2）已知坐标轴上有两动点P、Q同时出发，P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动，Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动，点Q到达A点整个运动随之结束．设运动时间为t（t＞0）秒．问：是否存在这样的t，使S△ODP＝S△ODQ，若存在，请求出t的值；若不存在，请说明理由．

    （3）点F是线段AC上一点，满足∠FOC＝∠FCO，点G是第二象限中一点，连OG，使得∠AOG＝∠AOF．点E是线段OA上一动点，连CE交OF于点H，当点E在线段OA上运动的过程中，的值是否会发生变化？若不变，请求出它的值；若变化，请说明理由．

    查看答案和解析>>

    同步练习册答案