
【题目】如图,以直角三角形AOC的直角顶点O为原点,以OC、OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足![]() .D为线段AC的中点.在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为
.D为线段AC的中点.在平面直角坐标系中,以任意两点P(x1,y1)、Q(x2,y2)为端点的线段中点坐标为![]() ,
,![]() .
.

(1)则A点的坐标为 ;点C的坐标为 .D点的坐标为 .
(2)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿x轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿y轴正方向移动,点Q到达A点整个运动随之结束.设运动时间为t(t>0)秒.问:是否存在这样的t,使S△ODP=S△ODQ,若存在,请求出t的值;若不存在,请说明理由.
(3)点F是线段AC上一点,满足∠FOC=∠FCO,点G是第二象限中一点,连OG,使得∠AOG=∠AOF.点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,![]() 的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出它的值;若变化,请说明理由.
【答案】(1)(0,4),(2,0),(1,2);(2)存在,t=1;(3)![]() 的值不变,其值为2.
的值不变,其值为2.
【解析】
(1)根据绝对值和算术平方根的非负性,求得a,b的值,再利用中点坐标公式即可得出答案;
(2)先得出CP=t,OP=2﹣t,OQ=2t,AQ=4﹣2t,再根据S△ODP=S△ODQ,列出关于t的方程,求得t的值即可;
(3)过H点作AC的平行线,交x轴于P,先判定OG∥AC,再根据角的和差关系以及平行线的性质,得出∠PHO=∠GOF=∠1+∠2,∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4,最后代入![]() 进行计算即可.
进行计算即可.
解:(1)∵![]() .
.
∴a﹣2b=0,b﹣2=0,
解得a=4,b=2,
∴A(0,4),C(2,0);
∴x=![]() =1,y=
=1,y=![]() =2,
=2,
∴D(1,2).
故答案为(0,4),(2,0),(1,2).
(2)如图1中,
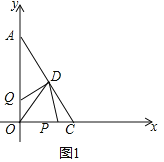
由条件可知:P点从C点运动到O点时间为2秒,Q点从O点运动到A点时间为2秒,
∴0<t≤2时,点Q在线段AO上,
即 CP=t,OP=2﹣t,OQ=2t,AQ=4﹣2t,
∴S△DOP=![]() OPyD=
OPyD=![]() (2﹣t)×2=2﹣t,S△DOQ=
(2﹣t)×2=2﹣t,S△DOQ=![]() OQxD=
OQxD=![]() ×2t×1=t,
×2t×1=t,
∵S△ODP=S△ODQ,
∴2﹣t=t,
∴t=1;
(3)![]() 的值不变,其值为2.理由如下:如图2中,
的值不变,其值为2.理由如下:如图2中,
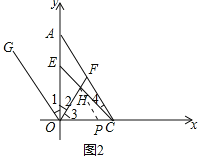
∵∠
又∵∠1=∠2,∠3=∠FCO,
∴∠GOC+∠ACO=180°,
∴OG∥AC,
∴∠1=∠CAO,
∴∠OEC=∠CAO+∠4=∠1+∠4,
如图,过H点作AC的平行线,交x轴于P,则∠4=∠PHC,PH∥OG,
∴∠PHO=∠GOF=∠1+∠2,
∴∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4,
∴![]() =
=![]() ,
,
=![]() ,
,
=2.


科目:初中数学 来源: 题型:
【题目】下列命题中:
①长为![]() 的线段
的线段![]() 沿某一方向平移
沿某一方向平移![]() 后,平移后线段
后,平移后线段![]() 的长为
的长为![]() ;
;
②三角形的高在三角形内部;
③六边形的内角和是外角和的两倍;
④平行于同一直线的两直线平行;
⑤两个角的两边分别平行,则这两个角相等,真命题个数有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)x2﹣4x+4=0
(2)x(x﹣2)=3(x﹣2)
(3)(2y﹣1)2﹣4=0
(4)(2x+1)(x﹣3)=0
(5)x2+5x+3=0
(6)x2﹣6x+1=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从邵阳市到长沙的高铁列车里程比普快列车里程缩短了75千米,运行时间减少了4小时,已知邵阳市到长沙的普快列车里程为306千米,高铁列车平均时速是普快列车平均时速的3.5倍.
(1)求高铁列车的平均时速;
(2)某日刘老师从邵阳火车南站到长沙市新大新宾馆参加上午11:00召开的会议,如果他买到当日上午9:20从邵阳市火车站到长沙火车南站的高铁票,而且从长沙火车南站到新大新宾馆最多需要20分钟.试问在高铁列车准点到达的情况下他能在开会之前赶到吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老王有一批货物要从A地运往B地准备租用某汽车运输公司的甲、乙两种货车若干辆,经了解,这两种货车两次运载货物的情况如下表所示:(每次都是满载)
第一次 | 第二次 | |
甲 | 2辆 | 5辆 |
乙 | 3辆 | 6辆 |
累计货运量 | 15.5t | 35t |
(1)甲、乙两种货车每辆各可运货物多少吨?
(2)现老王租用该公司甲货车3辆,乙货车5辆,刚好将这批货物运完(满载)若每吨货的运费为30元,则老王应付运费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰直角△ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求 ![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村老杨家有耕地和林地共24公顷,今年每公顷耕地纯收入为5500元,每公顷林地纯收入为6000元,耕地与林地的纯收入共137000元,为保护生态环境,增加收入,老杨计划将部分耕地改为林地(改后每公顷耕地,林地纯收入不变),要使改后的纯收入为140000元.问:
(1)老杨家原有耕地,林地各多少公顷?
(2)老杨应将多少公顷耕地改为林地?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=2,MN⊥AB于点M,且AM=BM,P是射线MN上一动点,E,D分别是PA,PB的中点,过点A,M,D的圆与BP的另一交点C(点C在线段BD上),连结AC,DE.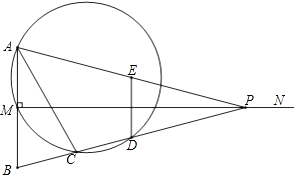
(1)当∠APB=28°时,求∠B和 ![]() 的度数;
的度数;
(2)求证:AC=AB.
(3)在点P的运动过程中
①当MP=4时,取四边形ACDE一边的两端点和线段MP上一点Q,若以这三点为顶点的三角形是直角三角形,且Q为锐角顶点,求所有满足条件的MQ的值;
②记AP与圆的另一个交点为F,将点F绕点D旋转90°得到点G,当点G恰好落在MN上时,连结AG,CG,DG,EG,直接写出△ACG和△DEG的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+b与反比例函数y= ![]() (k≠0)的图象相交于A(﹣1,4)、B(4,﹣1)两点,直线l⊥x轴于点E(﹣4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC
(k≠0)的图象相交于A(﹣1,4)、B(4,﹣1)两点,直线l⊥x轴于点E(﹣4,0),与反比例函数和一次函数的图象分别相交于点C、D,连接AC、BC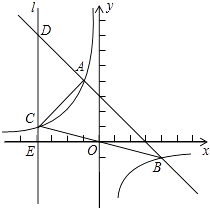
(1)求出b和k;
(2)求证:△ACD是等腰直角三角形;
(3)在y轴上是否存在点P,使S△PBC=S△ABC?若存在,请求出P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com