
【题目】将边长OA=8,OC=10的矩形OABC放在平面直角坐标系中,顶点O为原点,顶点C、A分别在![]() 轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。
轴和y轴上.在OA边上选取适当的点E,连接CE,将△EOC沿CE折叠。

(1)如图①,当点O落在AB边上的点D处时,点E的坐标为 ;
(2)如图②,当点O落在矩形OABC内部的点D处时,过点E作EG∥![]() 轴交CD于点H,交BC于点G.求证:EH=CH;
轴交CD于点H,交BC于点G.求证:EH=CH;
(3)在(2)的条件下,设H(m,n),写出m与n之间的关系式 ;
(4)如图③,将矩形OABC变为正方形,OC=10,当点E为AO中点时,点O落在正方形OABC内部的点D处,延长CD交AB于点T,求此时AT的长度。
【答案】(1)(0,5);(2)∠1=∠2.∵EG∥x轴,∴∠1=∠3. ∴∠2=∠3.∴EH=CH.
(3)![]() (4)
(4)![]() .
.
【解析】试题分析:(1)根据翻折变换的性质以及勾股定理得出BD的长,进而得出AE,EO的长即可得出答案;
(2)利用平行线的性质以及等角对等边得出答案即可;
(3)首先得出Rt△ATE≌Rt△DTE进而得出AT=DT.设AT=x,则BT=10-x,TC=10+x,在Rt△BTC中,BT2+BC2=TC2,求出即可.
试题解析:(1)∵将边长OA=8,OC=10的矩形OABC放在平面直角坐标系中,点O落在AB边上的点D处,
∴OC=DC=10,
∵BC=8,
∴BD=![]() =6,
=6,
∴AD=10-6=4,
设AE=x,则EO=8-x,
∴x2+42=(8-x)2,
解得:x=3,
∴AE=3,
则EO=8-3=5,
∴点E的坐标为:(0,5),
故答案为:(0,5);
(2)∵EG∥x轴,∴∠OCE=∠CEH,
由折叠可知∠OCE=∠ECH,
∴∠CEH=∠ECH,
∴EH=CH;
(3)连接ET,
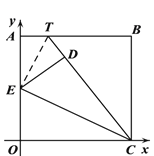
由题意可知,ED=EO,ED⊥TC,DC=OC=10,
∵E是AO中点,∴AE=EO,
∴AE=ED,
在Rt△ATE和Rt△DTE中,
![]() ,
,
∴Rt△ATE≌Rt△DTE(HL),
∴AT=DT,
设![]() ,则
,则![]() ,
,![]() ,
,
在Rt△BTC中,![]() ,
,
即![]() ,
,
解得![]() ,即
,即![]() .
.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】某路公交车从起点经过A、B、C、D站到达终点,一路上下乘客如下表所示。(用正数表示上车的人数,负数表示下车的人数)
| 起点 | A | B | C | D | 终点 |
上车的人数 | 18 | 15 | 12 | 7 | 5 | 0 |
下车的人数 | 0 | -3 | -4 | -10 | -11 |
(1)到终点下车还有_________ 人;
(2)车行驶在那两站之间车上的乘客最多?_______站和________站;
(3)若每人乘坐一站需买票1元,问该车出车一次能收入多少钱?写出算式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当你把纸对折一次时,可以得到2层,对折2次时可以得到4层,对折3次时可以得到8层,照这样折下去:
(1)你能发现层数与折纸次数的关系吗?
(2)计算对折5次时的层数;
(3)如果每层纸的厚度是0.05毫米,求对折10次之后纸的总厚度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,且经过点(0,2).有下列结论:
①ac>0;②b2﹣4ac>0;③a+c<2﹣b;④a<﹣![]() ;⑤x=﹣5和x=7时函数值相等.
;⑤x=﹣5和x=7时函数值相等.
其中正确的结论有( )
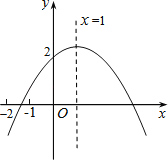
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
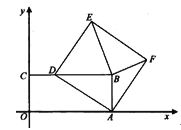
【题目】如图,在平面直角坐标系xoy中,矩形OABC的顶点B坐标为(12,5),点D在 CB边上从点C运动到点B,以AD为边作正方形ADEF,连BE、BF,在点D运动过程中,请探究以下问题:
(1)△ABF的面积是否改变,如果不变,求出该定值;如果改变,请说明理由;
(2)若△BEF为等腰三角形,求此时正方形ADEF的边长;
(3)设E(x,y),直接写出y关于x的函数关系式及自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类似乘方,我们把求若干个相同的不为零的有理数的除法运算叫做“除方”如2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等,并将2÷2÷2记作2③,读作“2的圈3次方”;(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作“﹣3的圈4次方”.
(1)直接写出结果:2③= ,(﹣3)④= ,(![]() )⑤= ,
)⑤= ,
(2)计算:24÷23+(﹣8)×2③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在有些情况下,不需要计算出结果也能把绝对值符号去掉.例如:|6+7|=6+7;|6﹣7|=7﹣6;|7﹣6|=7﹣6;|﹣6﹣7|=6+7
(1)根据上面的规律,把下列各式写成去掉绝对值符号的形式:
①|7﹣21|= ;②|﹣![]() ﹣0.8|= ;③|
﹣0.8|= ;③|![]() ﹣
﹣![]() |= :
|= :
(2)数a在数轴上的位置如图所示,则|a﹣2.5|= .
![]()
A.a﹣2.5
B.2.5﹣a
C.a+2.5
D.﹣a﹣2.5
(3)利用上述介绍的方法计算或化简:
①|![]() ﹣
﹣![]() |+|
|+|![]() ﹣
﹣![]() |﹣|﹣
|﹣|﹣![]() |+
|+![]() ;
;
②|![]() ﹣
﹣![]() |+|
|+|![]() ﹣
﹣![]() |﹣|﹣
|﹣|﹣![]() |+2(
|+2(![]() ),其中a>2.
),其中a>2.
查看答案和解析>>
科目:初中数学 来源: 题型:
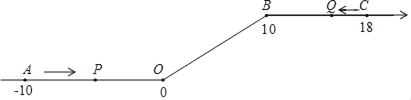
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位,动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半;点P从点A出发的同时,点Q从点C出发,以1单位/秒的速度沿着“折线数轴”的负方向运动,当点P到达B点时,点P、Q均停止运动.设运动的时间为t秒.问:
(1)用含t的代数式表示动点P在运动过程中距O点的距离;
(2)P、Q两点相遇时,求出相遇时间及相遇点M所对应的数是多少?
(3)是否存在P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等时?若存在,请直接写出t的取值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com