练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】当你把纸对折一次时，可以得到2层，对折2次时可以得到4层，对折3次时可以得到8层，照这样折下去：

    （1）你能发现层数与折纸次数的关系吗？

    （2）计算对折5次时的层数；

    （3）如果每层纸的厚度是0.05毫米，求对折10次之后纸的总厚度.

    【答案】（1）对折n次是层（2）32层（3）51.2毫米

    【解析】

    （1）由于把纸对折1次时，可以得到2层；当对折2次时，可以得到4-2层；当对折3次时，可以得到8-23层，由此即可得到层数5和折纸的次数之间的关系；

    （2）利用（1）的结论代入其中计算即可求解；

    （3）利用（1）的结论代入其中计算即可求解

    解：（1）对折一次是层，对折两次是层，对折n次层；

    （2）当时，.即对折5次时的层数为32层；

    （3）（毫米）.

    所以对折10次之后纸的总厚度是51.2毫米.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料：

    在学习“可化为一元一次方程的分式方程及其解法”的过程中，老师提出一个问题：若关于x的分式方程=1的解为正数，求a的取值范围．

    经过独立思考与分析后，小杰和小哲开始交流解题思路如下：

    小杰说：解这个关于x的分式方程，得x=a+4．由题意可得a+4＞0，所以a＞﹣4，问题解决．

    小哲说：你考虑的不全面，还必须保证x≠4，即a+4≠4才行．

    （1）请回答：　 　的说法是正确的，并简述正确的理由是　 　；

    （2）参考对上述问题的讨论，解决下面的问题：

    若关于x的方程的解为非负数，求m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在等边中，点在上，点在的延长线上，且.试探索以下问题：

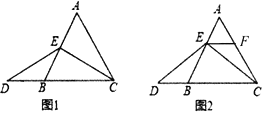
    (1)当点为的中点时，如图1，求证：.

    (2)如图2，当点不是的中点时，过点作，交于点，求证：是等边三角形.

    (3)在(2)的条件下，与还相等吗？请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

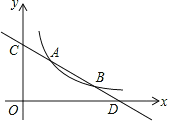
    【题目】直线y=kx+b与反比例函数y=（x＞0）的图象分别交于点 A（m，3）和点B（6，n），与坐标轴分别交于点C和点D．

    （1）求直线AB的解析式；

    （2）若点P是x轴上一动点，当△COD与△ADP相似时，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，有若干边长为1的正方形卡片，第1次并排摆2张黑色卡片，铺成一个长方形；第2次在黑色卡片上方和右侧摆白色卡片，所有卡片铺成了一个较大的长方形；第3次继续在白色卡片上方和右侧摆黑色卡片，所有卡片铺成了一个更大的长方形；以此类推，请解决以下问题：

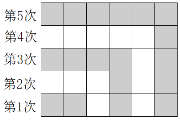
    （1）仅第10次要用去______张卡片,摆完第10次后，总共用去_______张卡片.

    （2）你知道 2+4+6+8+……+2n的结果是多少吗？写出结果，结合图形规律说明你的理由.

    （3）求出从第51次至第100次所摆卡片的数量之和.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知，，的垂直平分线交于，交于，则以下结论不正确的是（ ）

    A. B. ≌

    C. 是等腰三角形D. 射线是的角平分线

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】滴滴公布了新的滴滴快车计价规则，车费由“总里程费+总时长费”两部分构成，不同时段收费标准不同，具体收费标准如下表，如果车费不足起步价，则按起步价收费.

    时间段

    里程费（元/千米）

    时长费（元/分钟）

    起步价（元）

    06:00-10:00

    1.80

    0.80

    14.00

    10:00-17:00

    1.45

    0.40

    13.00

    17:00-21:00

    1.50

    0.80

    14.00

    21:00-6:00

    0.80

    0.80

    14.00

    （1）小明早上7:10乘坐滴滴快车上学，行车里程6千米，行车时间10分钟，则应付车费多少元？

    （2）小云17:10放学回家，行车里程2千米，行车时间12分钟，则应付车费多少元？

    （3）下晚自习后小明乘坐滴滴快车回家，20:45在学校上车，由于堵车，平均速度是千米/小时，15分钟后走另外一条路回家，平均速度是千米/小时，10分钟后到家，则他应付车费多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将边长OA=8，OC=10的矩形OABC放在平面直角坐标系中，顶点O为原点，顶点C、A分别在轴和y轴上.在OA边上选取适当的点E，连接CE，将△EOC沿CE折叠。

    （1）如图①，当点O落在AB边上的点D处时，点E的坐标为 ；

    （2）如图②，当点O落在矩形OABC内部的点D处时，过点E作EG∥轴交CD于点H，交BC于点G.求证：EH＝CH；

    （3）在（2）的条件下，设H（m，n），写出m与n之间的关系式 ；

    （4）如图③，将矩形OABC变为正方形，OC＝10，当点E为AO中点时，点O落在正方形OABC内部的点D处，延长CD交AB于点T，求此时AT的长度。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(12分)如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB于点D.点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．

    (1)求线段CD的长；

    (2)设△CPQ的面积为S，求S与t之间的函数关系式，并确定在运动过程中是否存在某一时刻t，使得S△CPQ∶S△ABC＝9∶100？若存在，求出t的值；若不存在，说明理由；

    (3)当t为何值时，△CPQ为等腰三角形？

    查看答案和解析>>

    同步练习册答案