
【题目】在等边![]() 中,点
中,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .试探索以下问题:
.试探索以下问题:
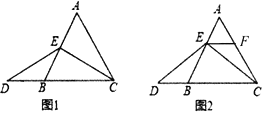
(1)当点![]() 为
为![]() 的中点时,如图1,求证:
的中点时,如图1,求证:![]() .
.
(2)如图2,当点![]() 不是
不是![]() 的中点时,过点
的中点时,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() 是等边三角形.
是等边三角形.
(3)在(2)的条件下,![]() 与
与![]() 还相等吗?请说明理由.
还相等吗?请说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)ED=EC.
【解析】
(1)根据等边三角形的性质得出AB=AC=BC,∠ABC=∠ACB=∠A=60°,再由E是AB的中点,AE=BE=BD,证出∠EDB=∠ECB,得出EC=ED;
(2)在△AEF中,只要证明有两个内角是60°即可;
(3)只要证明△DBE≌△EFC,即可推出结论.
解:(1)证明:∵△ABC是等边三角形,
∴AB=AC=BC,
∠ABC=∠ACB=∠A=60o ,
∵E是AB的中点,
∴AE=BE,∠ECB=![]() ∠ACB=30°,
∠ACB=30°,
∵AE=BD,
∴BE=BD,
∴∠EDB=∠DEB=![]() ∠ABC=30°,
∠ABC=30°,
∴∠EDB=∠ECB,
∴EC=ED.
(2)∵EF∥BC,
∴∠AEF=∠ABC=60 o,∠AFE=∠ACB=60°,
∴△AEF是等边三角形,
(3)ED=EC.理由如下:
由(2)得:△AEF是等边三角形
∴∠AFE=∠ABC=60°,AE=EF=AF
∴∠EFC=∠DBE=120°,
又∵AE=BD,AB=AC,
∴BD=EF,BE=FC,
∴△DBE≌△EFC(SAS),
∴ED=EC.


科目:初中数学 来源: 题型:
【题目】按下列要求画图,并回答问题.
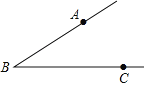
如图,已知∠ABC.
(1)在射线BC上戳取BD=BA,连接AD;
(2)画∠ABD的平分线交线段AD于点M.
回答问题:线段AM和线段DM的大小关系是:AM DM.∠AMB的度数为 度.(精确到1度).
(友情提醒:截取用圆规,并保留痕迹:画完图要下结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一个内角为90°,且对角线相等的四边形称为“不完全矩形”.
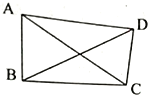
(1)①如图1,在不完全矩形![]() 中,
中,![]() ,若
,若![]() ,
,![]() ,则
,则![]() ____;
____;
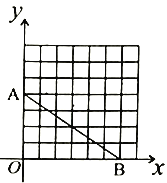
②如图2,在平面直角坐标系中,![]() ,
,![]() ,若整点
,若整点![]() 使得四边形
使得四边形![]() 是不完全矩形,则点
是不完全矩形,则点![]() 的坐标是_____;(整点指横坐标、纵坐标都为整数的点)
的坐标是_____;(整点指横坐标、纵坐标都为整数的点)
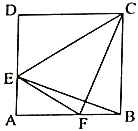
(2)如图3,在正方形![]() 中,点
中,点![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() ,求证:四边形
,求证:四边形![]() 是不完全矩形.
是不完全矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某路公交车从起点经过A、B、C、D站到达终点,一路上下乘客如下表所示。(用正数表示上车的人数,负数表示下车的人数)
| 起点 | A | B | C | D | 终点 |
上车的人数 | 18 | 15 | 12 | 7 | 5 | 0 |
下车的人数 | 0 | -3 | -4 | -10 | -11 |
(1)到终点下车还有_________ 人;
(2)车行驶在那两站之间车上的乘客最多?_______站和________站;
(3)若每人乘坐一站需买票1元,问该车出车一次能收入多少钱?写出算式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫作格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB'C′;
(2)画出△AB′C′向左平移4格后的△A′B″C″;
(3)计算线段AB在变换到AB′的过程中扫过区域的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A坐标为(6,0),点B在y轴的正半轴上,且![]() =240.
=240.
(1)求点B坐标;
(2)若点P从B出发沿y轴负半轴方向运动,速度每秒2个单位,运动时间t秒,△AOP的面积为S,求S与t的关系式,并直接写出t的取值范围;
(3)在(2)的条件下,若S△AOP:S△ABP=1:3,且S△AOP+S△ABP=S△AOB,在线段AB的垂直平分线上是否存在点Q,使得△AOQ的面积与△BPQ的面积相等?若存在,求出Q点坐标;若不存在,请说明理由。



查看答案和解析>>
科目:初中数学 来源: 题型:
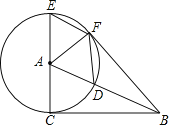
【题目】在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF,DF.
(1)试探究BF与AF位置关系,并说明理由;
(2)当∠CAB等于多少度时,四边形ADEF为菱形?请给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当你把纸对折一次时,可以得到2层,对折2次时可以得到4层,对折3次时可以得到8层,照这样折下去:
(1)你能发现层数与折纸次数的关系吗?
(2)计算对折5次时的层数;
(3)如果每层纸的厚度是0.05毫米,求对折10次之后纸的总厚度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类似乘方,我们把求若干个相同的不为零的有理数的除法运算叫做“除方”如2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等,并将2÷2÷2记作2③,读作“2的圈3次方”;(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)记作(﹣3)④,读作“﹣3的圈4次方”.
(1)直接写出结果:2③= ,(﹣3)④= ,(![]() )⑤= ,
)⑤= ,
(2)计算:24÷23+(﹣8)×2③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com