
【题目】在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF,DF.
(1)试探究BF与AF位置关系,并说明理由;
(2)当∠CAB等于多少度时,四边形ADEF为菱形?请给予证明.
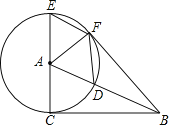
【答案】(1)互相垂直(2)60°
【解析】试题分析:(1)利用SAS可证得两△ABC≌△ABF,从而得∠AFB=∠ACB=90°,即可作出判断;
(2)若四边形ADFE为菱形,则四条边相等,因为EF=AE,AE=AF,所以△EAF为等边三角形,所以∠E=60°,所以∠CAB=∠E=60°.当∠CAB=60°时,可证AE∥FD,四边形ADFE是邻边相等的平行四边形,所以是菱形.
试题解析:(1)BF与AF位置关系为互相垂直,
理由如下:∵EF∥AB,∴∠E=∠CAB,∠EFA=∠FAB,
∵∠E=∠EFA,∴∠FAB=∠CAB,
在△ABC和△ABF中, 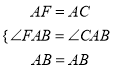 ,
,
∴△ABC≌△ABF(SAS),∴∠AFB=∠ACB=90°,
∴BF与AF位置关系为互相垂直;
(2)若四边形ADFE为菱形,则四条边相等,两组对边分别平行,∵EF=AE,AE=AF,
∴△EAF为等边三角形,∴∠E=60°,∴∠CAB=∠E=60°.
∴当∠CAB等于60度时,四边形ADFE为菱形.
证明如下:当∠CAB=60°时,∠FAB=60°,∠E=∠EFA=60°,∴∠EAF=∠AFD=60°,
∴AE∥FD,∵EF∥AD,∴四边形ADFE是平行四边形,又∵AE=AD,
∴四边形ADFE是邻边相等的平行四边形即菱形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知数轴上的点A和点B之间的距离为28个单位长度,点A在原点的左边,距离原点8个单位长度,点B在原点的右边.
(Ⅰ)求点A,点B对应的数;
(Ⅱ)数轴上点A以每秒1个单位长度出发向左移动,同时点B以每秒3个单位长度的速度向左移动,在点C处追上了点A,求点C对应的数.
(Ⅲ)已知在数轴上点M从点A出发向右运动,速度为每秒1个单位长度,同时点N从点B出发向右运动,速度为每秒2个单位长度,设线段NO的中点为P(O为原点),在运动的过程中,线段![]() 的值是否变化?若不变,请说明理由并求其值;若变化,请说明理由.
的值是否变化?若不变,请说明理由并求其值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,七年级某班男同学进行了100米测验,达标成绩为15秒,下表是梦想小组8名男生的成绩记录,其中“+”表示成绩大于15秒.
﹣0.8 | +1 | ﹣1.2 | 0 | ﹣0.7 | +0.6 | ﹣0.4 | ﹣0.1 |
问:(1)这个小组男生的达标率为多少?(达标率=![]() )
)
(2)这个小组男生的平均成绩是多少秒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边![]() 中,点
中,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .试探索以下问题:
.试探索以下问题:
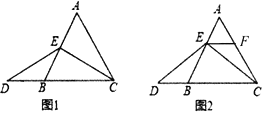
(1)当点![]() 为
为![]() 的中点时,如图1,求证:
的中点时,如图1,求证:![]() .
.
(2)如图2,当点![]() 不是
不是![]() 的中点时,过点
的中点时,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() 是等边三角形.
是等边三角形.
(3)在(2)的条件下,![]() 与
与![]() 还相等吗?请说明理由.
还相等吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选项目人数统计表
项目 | 男生(人数) | 女生(人数) |
机器人 | 7 | 9 |
3D打印 | m | 4 |
航模 | 2 | 2 |
其他 | 5 | n |
根据以上信息解决下列问题:
(1)m=_____,n=_____;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为_____°;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
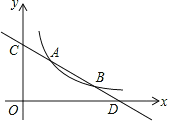
【题目】直线y=kx+b与反比例函数y=![]() (x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点 A(m,3)和点B(6,n),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,有若干边长为1的正方形卡片,第1次并排摆2张黑色卡片,铺成一个长方形;第2次在黑色卡片上方和右侧摆白色卡片,所有卡片铺成了一个较大的长方形;第3次继续在白色卡片上方和右侧摆黑色卡片,所有卡片铺成了一个更大的长方形;以此类推,请解决以下问题:
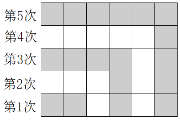
(1)仅第10次要用去______张卡片,摆完第10次后,总共用去_______张卡片.
(2)你知道 2+4+6+8+……+2n的结果是多少吗?写出结果,结合图形规律说明你的理由.
(3)求出从第51次至第100次所摆卡片的数量之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴公布了新的滴滴快车计价规则,车费由“总里程费+总时长费”两部分构成,不同时段收费标准不同,具体收费标准如下表,如果车费不足起步价,则按起步价收费.
时间段 | 里程费(元/千米) | 时长费(元/分钟) | 起步价(元) |
06:00-10:00 | 1.80 | 0.80 | 14.00 |
10:00-17:00 | 1.45 | 0.40 | 13.00 |
17:00-21:00 | 1.50 | 0.80 | 14.00 |
21:00-6:00 | 0.80 | 0.80 | 14.00 |
(1)小明早上7:10乘坐滴滴快车上学,行车里程6千米,行车时间10分钟,则应付车费多少元?
(2)小云17:10放学回家,行车里程2千米,行车时间12分钟,则应付车费多少元?
(3)下晚自习后小明乘坐滴滴快车回家,20:45在学校上车,由于堵车,平均速度是![]() 千米/小时,15分钟后走另外一条路回家,平均速度是
千米/小时,15分钟后走另外一条路回家,平均速度是![]() 千米/小时,10分钟后到家,则他应付车费多少元?
千米/小时,10分钟后到家,则他应付车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学报名次参加学校秋季运动会,有以下5个项目可供选择:径赛项目:100m、200m、1000m(分别用A1、A2、A3表示);田赛项目:跳远,跳高(分别用T1、T2表示)
(1)该同学从5个项目中任选一个,恰好是田赛项目的概率P为___________;
(2)该同学从5个项目中任选两个,求恰好是一个径赛项目和一个田赛项目的概率P1,利用列表法或树状图加以说明;
(3)该同学从5个项目中任选两个,则两个项目都是径赛项目的概率P2为___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com