
【题目】如图所示,有若干边长为1的正方形卡片,第1次并排摆2张黑色卡片,铺成一个长方形;第2次在黑色卡片上方和右侧摆白色卡片,所有卡片铺成了一个较大的长方形;第3次继续在白色卡片上方和右侧摆黑色卡片,所有卡片铺成了一个更大的长方形;以此类推,请解决以下问题:
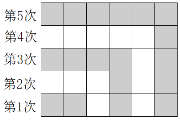
(1)仅第10次要用去______张卡片,摆完第10次后,总共用去_______张卡片.
(2)你知道 2+4+6+8+……+2n的结果是多少吗?写出结果,结合图形规律说明你的理由.
(3)求出从第51次至第100次所摆卡片的数量之和.
【答案】(1)20,110;(2)2+4+6+8+……+2n= n(n+1);(3)从第51次至第100次所摆卡片的数量之和7550.
【解析】
(1)观察图形可知:第1次共用去卡片2张,可以看成水平方向1张,竖直方向1张;第2次共用去卡片4张,可以看成水平方向2张,竖直方向2张;依次类推,可得:第n次共用去卡片2n张,可以看成水平方向n张,竖直方向n张.由此得到第10次共用去卡片20张,前10次共用去的卡片=2(1+2+3+……+9+10),计算即可.
(2)根据2+4+6+8+……+2n表示摆完第n次后共用去的卡片数.由图形可知:这些卡片共有n(n+1)张,即可得到结论;
(3) 用前100次用去的卡片数-前50次共用去的卡片数即可得到结论.
(1)观察图形可知:第1次共用去卡片2张,可以看成水平方向1张,竖直方向1张;
第2次共用去卡片4张,可以看成水平方向2张,竖直方向2张;
第3次共用去卡片6张,可以看成水平方向3张,竖直方向3张;
……
第n次共用去卡片2n张,可以看成水平方向n张,竖直方向n张.
由此得到第10次共用去卡片20张,前10次共用去卡片=2(1+2+3+……+9+10)=![]() =110.
=110.
故答案为:20,110.
(2)2+4+6+8+……+2n=n(n+1).
因为2+4+6+8+……+2n表示摆完第n次后共用去的卡片数.
根据图形可知:这些卡片共有n(n+1)张,
所以2+4+6+8+……+2n= n(n+1).
(3) 摆完第50次共用去50×(50+1)块卡片;
摆完第100次共用去100×(100+1)块卡片;
从第51次至第100次所摆卡片的数量之和为:
100×(100+1)-50×(50+1)=7550.
答:从第51次至第100次所摆卡片的数量之和7550.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4).
(1)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2.
(2)求点C1在旋转过程中所经过的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫作格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
(1)在正方形网格中,画出△AB'C′;
(2)画出△AB′C′向左平移4格后的△A′B″C″;
(3)计算线段AB在变换到AB′的过程中扫过区域的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
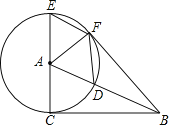
【题目】在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF,DF.
(1)试探究BF与AF位置关系,并说明理由;
(2)当∠CAB等于多少度时,四边形ADEF为菱形?请给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;…,根据以上操作,若要得到2011个小正方形,则需要操作的次数是( )
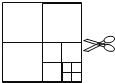
A. 669 B. 670 C. 671 D. 672
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当你把纸对折一次时,可以得到2层,对折2次时可以得到4层,对折3次时可以得到8层,照这样折下去:
(1)你能发现层数与折纸次数的关系吗?
(2)计算对折5次时的层数;
(3)如果每层纸的厚度是0.05毫米,求对折10次之后纸的总厚度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形OABC中,AB∥OC,∠OAB=90°, ∠OCB=60°,AB=2,OA=2![]() .
.
(1)如图①,连接OB,请直接写出OB的长度;
(2)如图②,过点O作OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度,设点P运动的时间为t秒,△OPQ的面积为S(平方单位).
①求S与t之间的函数关系式;
②设PQ与OB交于点M,当△OPM为等腰三角形时,试求出△OPQ的面积S的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=ax2+bx+c(a≠0)的图象的对称轴是直线x=1,且经过点(0,2).有下列结论:
①ac>0;②b2﹣4ac>0;③a+c<2﹣b;④a<﹣![]() ;⑤x=﹣5和x=7时函数值相等.
;⑤x=﹣5和x=7时函数值相等.
其中正确的结论有( )
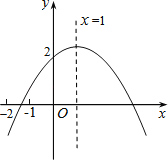
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
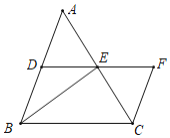
【题目】如图,在△ABC中,点D,E分别是边AB,AC的中点,过点C作CF∥AB交DE的延长线于点F,连接BE.
(1)求证:四边形BCFD是平行四边形.
(2)当AB=BC时,若BD=2,BE=3,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com