
ЎҫМвДҝЎҝИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬өгAЧшұкОӘ(6Ј¬0)Ј¬өгBФЪyЦбөДХэ°лЦбЙПЈ¬ЗТ![]() =240.
=240.
(1)ЗуөгBЧшұкЈ»
(2)ИфөгPҙУBіц·ўСШyЦбёә°лЦб·ҪПтФЛ¶ҜЈ¬ЛЩ¶ИГҝГл2ёцөҘО»Ј¬ФЛ¶ҜКұјдtГлЈ¬ЎчAOPөДГж»эОӘSЈ¬ЗуSУлtөД№ШПөКҪЈ¬ІўЦұҪУРҙіцtөДИЎЦө·¶О§Ј»
(3)ФЪ(2)өДМхјюПВЈ¬ИфSЎчAOPЈәSЎчABP=1:3Ј¬ЗТSЎчAOP+SЎчABP=SЎчAOBЈ¬ФЪПЯ¶ОABөДҙ№ЦұЖҪ·ЦПЯЙПКЗ·сҙжФЪөгQЈ¬К№өГЎчAOQөДГж»эУлЎчBPQөДГж»эПаөИЈҝИфҙжФЪЈ¬ЗуіцQөгЧшұкЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЎЈ



Ўҫҙр°ёЎҝЈЁ1Ј©өг BөДЧшұкОӘЈЁ0,8Ј©ЈЁ2Ј©S=24-6t (0ЎЬt<4)Ј» S=6t-24(t>4)Ј»(3)өгQөДЧшұкОӘ(-1,1)»тЈЁ7,7Ј©.
ЎҫҪвОцЎҝКФМв·ЦОцЈәЈЁ1Ј©ёщҫЭИэҪЗРОөДГж»э№«КҪЗуіцOBөДіӨјҙҝЙЈ»
ЈЁ2Ј©·Ц0ЎЬt<4әНtЎЭ4БҪЦЦЗйҝцЈ¬ёщҫЭИэҪЗРОГж»э№«КҪјЖЛгјҙҝЙЈ»
ЈЁ3Ј©ёщҫЭМвТвәНИэҪЗРОөДГж»э№«КҪЗуіцOPЎўBPөДіӨЈ¬ёщҫЭПаЛЖИэҪЗРОөДРФЦКЗуіцөгEөДЧшұкЈ¬ёщҫЭЦРөгөДРФЦКИ·¶ЁөгFөДЧшұкЈ¬ФЛУГҙэ¶ЁПөКэ·ЁЗуіцЦұПЯefөДҪвОцКҪЈ¬ёщҫЭөИөЧөДБҪёцИэҪЗРОГж»эПаөИЈ¬ЛьГЗөДёЯТІПаөИ·Цx=yәНx=-yБҪЦЦЗйҝцјЖЛгјҙҝЙЈ®
КФМвҪвОцЈәЈЁ1Ј©ЎЯөг![]() ЧшұкОӘ
ЧшұкОӘ![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
![]() Ј¬
Ј¬
Фт![]() Ј¬
Ј¬
![]() өг BөДЧшұкОӘЈЁ0,8Ј©Ј»
өг BөДЧшұкОӘЈЁ0,8Ј©Ј»
ЈЁ2Ј©өұ0ЎЬt<4КұЈ¬S=![]() ЎБЈЁ8-2tЈ©ЎБ6=24-6tЈ»
ЎБЈЁ8-2tЈ©ЎБ6=24-6tЈ»
өұt>4КұЈ¬S=![]() ЈЁ2t-8Ј©ЎБ6=6t-24Ј»
ЈЁ2t-8Ј©ЎБ6=6t-24Ј»
(3) ![]()
ПЯ¶О![]() өДҙ№ЦұЖҪ·ЦПЯҪ»
өДҙ№ЦұЖҪ·ЦПЯҪ»![]() УЪ
УЪ![]() ,Ҫ»
,Ҫ»![]() УЪ
УЪ![]() Ј¬
Ј¬
УЙ№ҙ№Й¶ЁАнЈ¬ ![]() ,Фтөг
,Фтөг![]() өДЧшұкОӘ
өДЧшұкОӘ![]()
![]() өг
өг![]() өДЧшұкОӘ
өДЧшұкОӘ![]()
ҪвөГЦұПЯ![]() өДҪвОцКҪОӘ
өДҪвОцКҪОӘ![]()
![]()
![]() өг
өг![]() өДЧшұкОӘ(-1,1)»тЈЁ7,7Ј©
өДЧшұкОӘ(-1,1)»тЈЁ7,7Ј©



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіЙМіЎПъКЫТ»ЕъГыЕЖіДТВЈ¬ЖҪҫщГҝМмҝЙКЫіц20јюЈ¬ГҝјюіДТВУҜАы40ФӘЈ®ОӘБЛА©ҙуПъКЫЈ¬ФцјУ
УҜАыЈ¬ҫЎҝмјхЙЩҝвҙжЈ¬ЙМіЎҫц¶ЁІЙИЎККөұөДҪөјЫҙлК©Ј®ҫӯөчІй·ўПЦЈ¬Из№ыГҝјюіДТВҪөјЫ1ФӘЈ¬ЙМіЎЖҪҫщГҝМм
ҝЙ¶аКЫіц2јюЈ®
ЈЁ1Ј©ИфЙМіЎЖҪҫщГҝМмУҜАы1200ФӘЈ¬ГҝјюіДТВУҰҪөјЫ¶аЙЩФӘЈҝ
ЈЁ2Ј©ИфТӘК№ЙМіЎЖҪҫщГҝМмөДУҜАыЧо¶аЈ¬ЗлДгОӘЙМіЎЙијЖҪөјЫ·Ҫ°ёЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЎчABCЦРЈ¬ЎПACB=90ЎгЈ¬AC=BCЈ¬ЦұПЯMNҫӯ№эөгCЈ¬ЗТADЎНMNУЪDЈ¬BEЎНMNУЪE.
ЈЁ1Ј©өұЦұПЯMNИЖөгCРэЧӘөҪНј1өДО»ЦГКұЈ¬ЗуЦӨЈәDE=AD+BEЈ»
ЈЁ2Ј©өұЦұПЯMNИЖөгCРэЧӘөҪНј2өДО»ЦГКұЈ¬ЗуЦӨЈәDE=AD-BEЈ»
ЈЁ3Ј©өұЦұПЯMNИЖөгCРэЧӘөҪНј3өДО»ЦГКұЈ¬КФОКDEЎўADЎўBEҫЯУРФхСщөДөИБҝ№ШПөЈҝЗлЦұҪУРҙіцХвёцөИБҝ№ШПө.

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
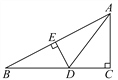
ЎҫМвДҝЎҝИзНјЈ¬ФЪЎчABCЦРЈ¬ЎПCЈҪ90ЎгЈ¬DEҙ№ЦұЖҪ·ЦABЈ¬Ҫ»BCУЪөгDЈ¬Б¬ҪУADЈ¬ИфACЈҪ8Ј¬DCЈәADЈҪ3Јә5.ЗуЈә
(1)CDөДіӨЈ»
(2)DEөДіӨЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝПВБРјёЦЦРОЧҙөДҙЙЧ©ЦРЈ¬Ц»УГТ»ЦЦІ»ДЬ№»ЖМВъөШГжөДКЗЈЁЎЎЎЎЈ©
A.ХэБщұЯРО
B.ХэОеұЯРО
C.Хэ·ҪРО
D.ХэИэҪЗРО
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬ТСЦӘөИұЯИэҪЗРОABCөДұЯіӨОӘ3Ј¬№эABұЯЙПТ»өгPЧчPE![]() ACУЪөгEЈ¬QОӘBCСУіӨПЯЙПТ»өгЈ¬ИЎPA=CQЈ¬Б¬ҪУPQЈ¬Ҫ»ACУЪMЈ¬ФтEMөДіӨОӘ_________________.
ACУЪөгEЈ¬QОӘBCСУіӨПЯЙПТ»өгЈ¬ИЎPA=CQЈ¬Б¬ҪУPQЈ¬Ҫ»ACУЪMЈ¬ФтEMөДіӨОӘ_________________.

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИфУГН¬Т»ЦЦХэ¶аұЯРОҙЙЧ©ЖМөШГжЈ¬І»ДЬГЬЖМөШГжөДХэ¶аұЯРОКЗЈЁЎЎЎЎЈ©
A.Хэ°ЛұЯРО
B.ХэБщұЯРО
C.ХэЛДұЯРО
D.ХэИэұЯРО
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
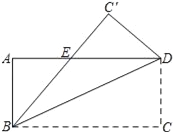
ЎҫМвДҝЎҝИзНјЈ¬Ҫ«іӨ·ҪРОABCDСШЧЕ¶ФҪЗПЯBDХЫөюЈ¬К№өгCВдФЪCЎдҙҰЈ¬BCЎдҪ»ADУЪөгEЈ®
ЈЁ1Ј©КФЕР¶ПЎчBDEөДРОЧҙЈ¬ІўЛөГчАнУЙЈ»
ЈЁ2Ј©ИфAB=3Ј¬AD=9Ј¬ЗуЎчBDEөДГж»э.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИз№ыөгPЈЁ3Ј¬y1Ј©Ј¬QЈЁ2Ј¬y2Ј©ФЪТ»ҙОәҜКэy=2x©Ғ1өДНјПуЙПЈ¬Фтy1Ј¬y2өДҙуРЎ№ШПөКЗЈЁЎЎЎЎЈ©
A. y1Јҫy2 B. y1Јјy2 C. y1=y2 D. ОЮ·ЁИ·¶Ё
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com