
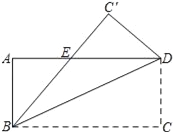
【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若AB=3,AD=9,求△BDE的面积.
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△DAC,△EBC均是等边三角形,点A,C,B在同一条直线上,AE,BD分别与CD,CE交于点M,N,下列结论:①△ACE≌△DCB; ②CM=CN;③AC=DN ;④∠DAE=∠DBC.其中正确的结论有________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A坐标为(6,0),点B在y轴的正半轴上,且![]() =240.
=240.
(1)求点B坐标;
(2)若点P从B出发沿y轴负半轴方向运动,速度每秒2个单位,运动时间t秒,△AOP的面积为S,求S与t的关系式,并直接写出t的取值范围;
(3)在(2)的条件下,若S△AOP:S△ABP=1:3,且S△AOP+S△ABP=S△AOB,在线段AB的垂直平分线上是否存在点Q,使得△AOQ的面积与△BPQ的面积相等?若存在,求出Q点坐标;若不存在,请说明理由。



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.动点P从点A开始沿折线AC-CB-BA运动,点P在AC,CB,BA边上运动的速度分别为每秒3,4,5个单位.直线l从与AC重合的位置开始,以每秒![]() 个单位的速度沿CB方向移动,移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P和直线l同时停止运动.
个单位的速度沿CB方向移动,移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P和直线l同时停止运动.
(1)当t=5秒时,点P走过的路径长为_________;当t=_________秒时,点P与点E重合;
(2)当点P在AC边上运动时,连结PE,并过点E作AB的垂线,垂足为H. 若以C、P、E为顶点的三角形与△EFH相似,试求线段EH的值;
(3)当点P在折线AC-CB-BA上运动时,作点P关于直线EF的对称点Q.在运动过程中,若形成的四边形PEQF为菱形,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A.3a+4b=12a
B.(ab3)2=ab6
C.(5a2﹣ab)﹣(4a2+2ab)=a2﹣3ab
D.x12÷x6=x2
查看答案和解析>>
科目:初中数学 来源: 题型:
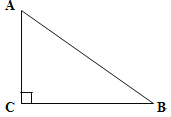
【题目】如图,已知△ABC,∠C=90,AC<BC,D为BC上一点,且到A,B两点的距离相等.
(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,则∠CAD=_________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com