
����Ŀ����ͼ����Rt��ABC�У���C��90�㣬AC��6��BC��8������P�ӵ�A��ʼ������AC��CB��BA�˶�����P��AC��CB��BA�����˶����ٶȷֱ�Ϊÿ��3��4��5����λ��ֱ��l����AC�غϵ�λ�ÿ�ʼ����ÿ��![]() ����λ���ٶ���CB�����ƶ����ƶ������б���l��AC���ҷֱ���CB��AB�߽���E��F���㣬��P��ֱ��lͬʱ���������˶���ʱ��Ϊt�룬����P��һ�λص���Aʱ����P��ֱ��lͬʱֹͣ�˶���
����λ���ٶ���CB�����ƶ����ƶ������б���l��AC���ҷֱ���CB��AB�߽���E��F���㣬��P��ֱ��lͬʱ���������˶���ʱ��Ϊt�룬����P��һ�λص���Aʱ����P��ֱ��lͬʱֹͣ�˶���
��1����t��5��ʱ����P�߹���·����Ϊ_________����t��_________��ʱ����P���E�غϣ�
��2������P��AC�����˶�ʱ������PE��������E��AB�Ĵ��ߣ�����ΪH. ����C��P��EΪ��������������EFH���ƣ������߶�EH��ֵ��
��3������P������AC��CB��BA���˶�ʱ������P����ֱ��EF�ĶԳƵ�Q�����˶������У����γɵ��ı���PEQFΪ���Σ���t��ֵ��

���𰸡���1��19��3 ����2��EH=![]() ��
��![]() ����3������Ҫ���tֵΪt��
����3������Ҫ���tֵΪt��![]() ��
�� ![]()
����������1��19��3
��2��ע���EFHΪֱ�DZ�3:4��ֱ�������Σ�����CPE��֮���ƣ�ҲӦ���.
��CP��6��3t��CE��![]() t���ֱ���CP:CE��3:4��4:3�����t��
t���ֱ���CP:CE��3:4��4:3�����t��![]() ��
��![]()
��t��![]() ʱ��EH��
ʱ��EH��![]() ����t��
����t��![]() ʱ��EH��
ʱ��EH��![]()
��3������P��AC���˶�ʱ�����ı���PEQFΪ���Σ�����PQ����PQ��ֱƽ��EF.
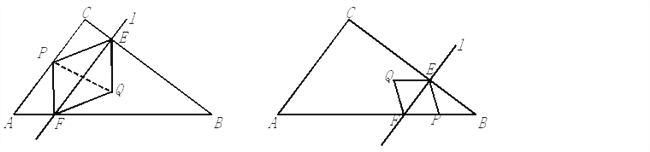
����EF��2CP������![]() (8��
(8��![]() t)��2(6��3t)�����t��
t)��2(6��3t)�����t��![]() ��2������
��2������
���� P��CB���˶�ʱ����Ȼ�������ı���.
���� P��BA���˶�ʱ�����ı���PEQFΪ���Σ���4��t��![]() ����PE��PF.
����PE��PF.
��Rt��BEF�У���֪PΪBF���е㣬����BF��2BP������![]() (8��
(8��![]() t)��2��5(t��4)��
t)��2��5(t��4)��
���t��![]() ��Ҳ����
��Ҳ����
��������������Ҫ���tֵ��������t��![]() ��
��![]()


 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺��һ����Ʒ��ÿ����Ʒ����30Ԫ�������з���������Ʒÿ���������y��������ÿ�����ۼ�x��Ԫ���Ĺ�ϵ�������£�
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
��1����֪y��x����һ�κ�����ϵ�������ϱ������y��x֮��Ĺ�ϵʽ����д���Ա���x��ȡֵ��Χ����
��2������̵�����������Ʒ��ÿ��Ҫ���150Ԫ������ôÿ����Ʒ�����ۼ�Ӧ��Ϊ����Ԫ��
��3������̵�ÿ������������Ʒ��������Ϊw��Ԫ�������w��x֮��Ĺ�ϵʽ�������ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����״�Ĵ�ש�У�ֻ��һ�ֲ��ܹ�����������ǣ�������
A.��������
B.�������
C.������
D.��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͬһ��������δ�ש�̵��棬�������̵������������ǣ�������
A.���˱���
B.��������
C.���ı���
D.��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ʦ����˶��ֻ����п��߶��������ζ������������±������һ�ζ�����ȣ�����ʦ�ڶ��ζ������������İٷ�������ƽ�����������İٷ��ʵ�3�������ݾ�����֪����ʦ�ڶ��ζ���ʱƽ�����������İٷ���С��0.5��
��Ŀ | ��һ�ζ��� | �ڶ��ζ��� | ||
���������� | 10000 | �� | ||
ƽ����������/���� | 0.6 | �� | ||
���루�ף� | 6000 | 7020 |
ע��������ƽ�����������룮
��1��������ʦ�ڶ��ζ���ʱƽ���������ٵİٷ��ʣ�
��2������ʦ���ֺ����в���������һΪ24000������������ζ���������������500�ף�ʹ���ܲ���ǡ��Ϊ24000����������ʦ��500��ƽ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
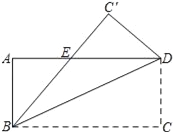
����Ŀ����ͼ����������ABCD���ŶԽ���BD�۵���ʹ��C����C������BC����AD�ڵ�E��
��1�����ж���BDE����״����˵�����ɣ�
��2����AB=3��AD=9������BDE�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е������ʺ���ȫ�������ǣ� ��
A.�����ܰɣ��ֵ�����Ŀ��������
B.��������ɻ����ÿ��Ƿ����Υ����Ʒ
C.ij��Ʒ�ƽ��ܵƵ�ʹ������
D.�˽�ӱ�ʡ��ѧ�������Ķ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��һ�κ���y1=kx+b��ͼ���뷴��������y2=![]() ��ͼ����A����2��n����B��1����3�����㣮
��ͼ����A����2��n����B��1����3�����㣮
��1����ȷ������һ�κ����ͷ����������ı���ʽ��
��2�����AOB�������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com