
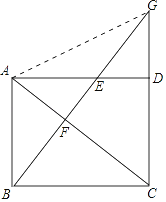
【题目】已知:如图,在平行四边形ABCD中,AC为对角线,E是边AD上一点,BE⊥AC交AC于点F,BE、CD的延长线交于点G,且∠ABE=∠CAD.
(1)求证:四边形ABCD是矩形;
(2)如果AE=EG,求证:AC2=BCBG.
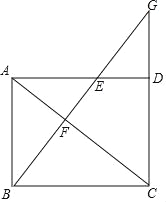
【答案】(1)见解析;(2)见解析.
【解析】
(1)、因为四边形ABCD是平行四边形,所以只要证明∠BAD=90°,即可得到四边形ABCD是矩形;(2)、连接AG,由平行四边形的性质和矩形的性质以及结合已知条件可证明△BCG∽△ABC,再由相似三角形的性质:对应边的比值相等即可证明AC2=BCBG.
(1)、解:证明: ∵BE⊥AC, ∴∠AFB=90°.
∴∠ABE+∠BAF=90°. ∵∠ABE=∠CAD. ∴∠CAD+∠BAF=90°. 即∠BAD=90°.
∵四边形ABCD是平行四边形, ∴四边形ABCD是矩形;
(2)、解:连接AG. ∵AE=EG, ∴∠EAG=∠EGA, ∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC, ∴∠ABG=∠BGC, ∴∠CAD=∠BGC, ∴∠AGC=∠GAC,
∴CA=CG, ∵AD∥BC, ∴∠CAD=∠ACB, ∴∠ACB=∠BGC,
∵四边形ABCD是矩形, ∴∠BCG=90°, ∴∠BCG=∠ABC, ∴△BCG∽△ABC,
∴ ![]() , ∴AC2=BCBG.
, ∴AC2=BCBG.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一种商品按销售量分三部分制定销售单价,如下表:
销售量 | 单价 |
不超过100件的部分 | 2.8元/件 |
超过100件不超过300件的部分 | 2.2元/件 |
超过300件的部分 | 2元/件 |
(1)若买100件花 元,买300件花 元;买380件花 元;
(2)小明买这种商品花了500元,求购买了这种商品多少件;
(3)若小明花了n元(n>280),恰好购买0.4n件这种商品,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
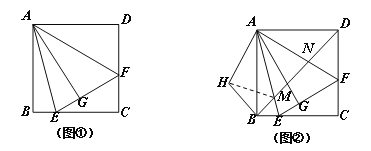
【题目】如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,
(1)求∠EAF的度数;
(2)在图①中,连结BD分别交AE、AF于点M、N,将△ADN绕点A顺时针旋转90°至△ABH位置,连结MH,得到图②.求证:MN2=MB2+ ND2 ;
(3)在图②中,若AG=12, BM=![]() ,直接写出MN的值.
,直接写出MN的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,小慧同学利用直尺和规进行了如下操作:①连接AC,分别以点A、C为圆心,以大于![]() AC的长为半径画弧,两弧相交于点P、Q;②作直线PQ,分别交BC、AC、AD于点E、O、F,连接AE、CF.根据操作结果,解答下列问题:
AC的长为半径画弧,两弧相交于点P、Q;②作直线PQ,分别交BC、AC、AD于点E、O、F,连接AE、CF.根据操作结果,解答下列问题:
(1)线段AF与CF的数量关系是 .
(2)若∠BAD=120°,AE平分∠BAD,AB=8,求四边形AECF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
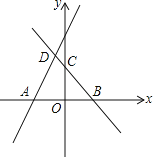
【题目】如图,直线y=![]() x+m与x轴交于点A(-3,0),直线y=-x+2与x轴、y轴分别交于B、C两点,并与直线y=
x+m与x轴交于点A(-3,0),直线y=-x+2与x轴、y轴分别交于B、C两点,并与直线y=![]() x+m相交于点D,
x+m相交于点D,
(1)点D的坐标为 ;
(2)求四边形AOCD的面积;
(3)若点P为x轴上一动点,当PD+PC的值最小时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)下面两个立体图形的名称是:__________,__________
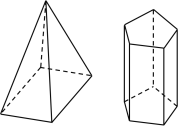
(2)一个立体图形的三视图如下图所示,这个立体图形的名称是__________

(3)画出下面立体图形的主视图.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为一棵大树,在树上距地面10 米的D处有两只猴子,他们同时发现C处有一筐水果,一只猴子从D处往上爬到树顶A处,又沿滑绳AC滑到C处,另一只猴子从D滑到B,再由B跑到C处,已知两只猴子所经路程都为40米,求树高AB.
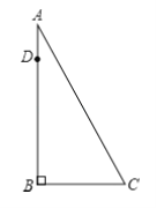
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.
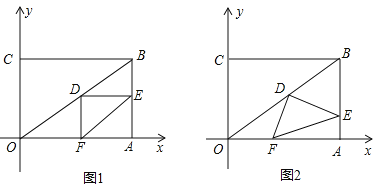
(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com