
【题目】在直角坐标系中,过原点O及点A(8,0),C(0,6)作矩形OABC、连结OB,点D为OB的中点,点E是线段AB上的动点,连结DE,作DF⊥DE,交OA于点F,连结EF.已知点E从A点出发,以每秒1个单位长度的速度在线段AB上移动,设移动时间为t秒.
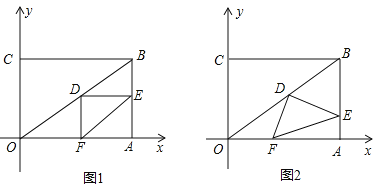
(1)如图1,当t=3时,求DF的长.
(2)如图2,当点E在线段AB上移动的过程中,∠DEF的大小是否发生变化?如果变化,请说明理由;如果不变,请求出tan∠DEF的值.
(3)连结AD,当AD将△DEF分成的两部分的面积之比为1:2时,求相应的t的值.
【答案】(1)3;(2)∠DEF的大小不变,tan∠DEF=![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】试题(1)当t=3时,点E为AB的中点,由三角形的中位线定理得出DE∥EA,DE=![]() OA=4,再由矩形的性质证出DE⊥AB,得出∠OAB=∠DEA=90°,证出四边形DFAE是矩形,得出DF=AE=3即可;
OA=4,再由矩形的性质证出DE⊥AB,得出∠OAB=∠DEA=90°,证出四边形DFAE是矩形,得出DF=AE=3即可;
(2)作DM⊥OA于点M,DN⊥AB于N,证明四边形DMAN是矩形,得出∠MDN=90°,DM∥AB,DN∥OA,由平行线得出比例式![]() ,
,![]() ,由三角形中位线定理得出DM=
,由三角形中位线定理得出DM=![]() AB=3,DN=
AB=3,DN=![]() OA=4,证明ΔDMF∽ΔDNE,得出
OA=4,证明ΔDMF∽ΔDNE,得出![]() ,再由三角函数的定义即可得解;
,再由三角函数的定义即可得解;
(3)作DM⊥OA于M,DN⊥AB于N,若AD将ΔDEF的面积分为1:2的两部分,设AD交EF于点G,则点G为EF的三等分点.
①当点E到达中点之前时,NE=3-t,由ΔDMF∽ΔDNE得:MF=![]() ,求出AF=4+MF=
,求出AF=4+MF=![]() ,得出G(
,得出G(![]() ,
,![]() ),求出直线AD的解析式为y=-
),求出直线AD的解析式为y=-![]() +6,把G(
+6,把G(![]() ,
,![]() )代入即可求出t的值;
)代入即可求出t的值;
②当点超过中点之后,NE=t-3,由由ΔDMF∽ΔDNE得:MF=![]() ,求出AF=4-MF=
,求出AF=4-MF=![]() ,得出G(
,得出G(![]() ,
,![]() ),代入直线AD的解析式y=-
),代入直线AD的解析式y=-![]() +6即可求出t的值;
+6即可求出t的值;
试题解析: (1)当t=3时,点E为AB的中点,
∵A(8,0),C(0,6),
∴OA=8,OC=6,
∵点D为OB的中点,
∴DE∥OA,DE=![]() OA=4,
OA=4,
∵四边形OABC是矩形,
∴OA⊥AB,
∴DE⊥AB,
∴∠OAB=∠DEA=90°,
又∵DF⊥DE,
∴∠EDF=90°,
∴四边形DFAE是矩形,
∴DF=AE=3;
(2)∠DEF的大小不变;理由如下:
作DM⊥OA于M,DN⊥AB于N,如图2所示:
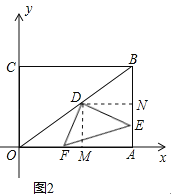
∵四边形OABC是矩形,
∴OA⊥AB,
∴四边形DMAN是矩形,
∴∠MDN=90°,DM∥AB,DN∥OA,
∴![]() ,
,![]() ,
,
∵点D为OB的中点,
∴M、N分别是OA、AB的中点,
∴DM=![]() AB=3,DN=
AB=3,DN=![]() OA=4,
OA=4,
∵∠EDF=90°,
∴∠FDM=∠EDN,
又∵∠DMF=∠DNE=90°,
∴△DMF∽△DNE,
∴![]() ,
,
∵∠EDF=90°,
∴tan∠DEF=![]() ;
;
(3)作DM⊥OA于M,DN⊥AB于N,
若AD将△DEF的面积分成1:2的两部分,
设AD交EF于点G,则点G为EF的三等分点;
①当点E到达中点之前时,如图3所示,NE=3﹣t,
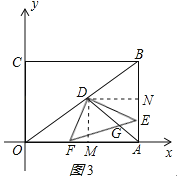
由△DMF∽△DNE得:MF=![]() (3﹣t),
(3﹣t),
∴AF=4+MF=﹣![]() t+
t+![]() ,
,
∵点G为EF的三等分点,
∴G(![]() ,
,![]() ),
),
设直线AD的解析式为y=kx+b,
把A(8,0),D(4,3)代入得:![]() ,
,
解得: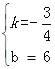 ,
,
∴直线AD的解析式为y=﹣![]() x+6,
x+6,
把G(![]() ,
,![]() )代入得:t=
)代入得:t=![]() ;
;
②当点E越过中点之后,如图4所示,NE=t﹣3,
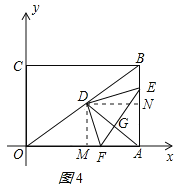
由△DMF∽△DNE得:MF=![]() (t﹣3),
(t﹣3),
∴AF=4﹣MF=﹣![]() t+
t+![]() ,
,
∵点G为EF的三等分点,
∴G(![]() ,
,![]() ),
),
代入直线AD的解析式y=﹣![]() x+6得:t=
x+6得:t=![]() ;
;
综上所述,当AD将△DEF分成的两部分的面积之比为1:2时,t的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
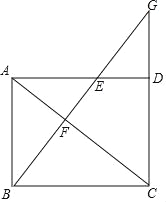
【题目】已知:如图,在平行四边形ABCD中,AC为对角线,E是边AD上一点,BE⊥AC交AC于点F,BE、CD的延长线交于点G,且∠ABE=∠CAD.
(1)求证:四边形ABCD是矩形;
(2)如果AE=EG,求证:AC2=BCBG.
查看答案和解析>>
科目:初中数学 来源: 题型:
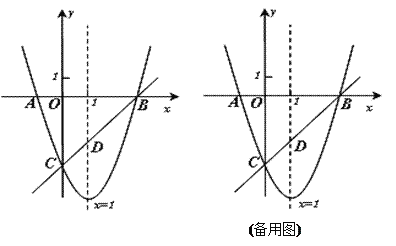
【题目】如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.
⑴求抛物线的函数表达式;
⑵求直线BC的函数表达式;
⑶点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P在第三象限.①当线段PQ=![]() AB时,求tan∠CED的值;②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
AB时,求tan∠CED的值;②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,C为BA延长线上一点,CD切半圆O于点D。连结OD,作BE⊥CD于点E,交半圆O于点F。已知CE=12,BE=9,
(1)求证:△COD∽△CBE;
(2)求半圆O的半径的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某楼盘一楼是车库(暂不销售),二楼至二十三楼均为商品房(对外销售).商品房售价方案如下:第八层售价为3000元/米2,从第八层起每上升一层,每平方米的售价增加40元;反之,楼层每下降一层,每平方米的售价减少20元.已知商品房每套面积均为120平方米.开发商为购买者制定了两种购房方案:
方案一:购买者先交纳首付金额(商品房总价的30%),再办理分期付款(即贷款).
方案二:购买者若一次付清所有房款,则享受8%的优惠,并免收五年物业管理费(已知每月物业管理费为a元)
【1】![]() 函数解析式;
函数解析式;
【2】小张已筹到120000元,若用方案一购房,他可以购买哪些楼层的商品房呢?
【3】有人建议老王使用方案二购买第十六层,但他认为此方案还不如不免收物业管理费而直接享受9%的优惠划算.你认为老王的说法一定正确吗?请用具体的数据阐明你的看法。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】微信“抢红包”游戏现在受到越来越多的人喜欢,其中有一种玩法“拼手气红包”,用户设置好总金额以及红包个数后,可以随机生成金额不等的红包,现有一用户发了三个“拼手气红包”,总金额为5元,随机被甲、乙、丙三人抢到。
(1)下列事件中,确定事件是__________。
①甲、乙两人抢到的红包金额之和比丙抢到的红包金额多;
②甲抢到的金额为0.5元的红包;
③乙抢到金额为6元的红包。
(2)随机红包分为大、中、小三个金额,用画树状图或列表的方法求出连抽两次最大金额的红包概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠B=40°,求∠AGD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C处有一些蜂蜜,此时一只蚂蚁正好也在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,那么蚂蚁要吃到甜甜的蜂蜜所爬行的最短距离是( )

A.13B.14C.15D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
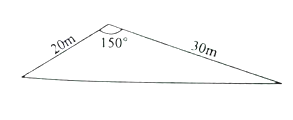
【题目】我市在旧城改造中,计划在市内一块如下图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价![]() 元,则购买这种草皮至少需要______元.
元,则购买这种草皮至少需要______元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com