练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

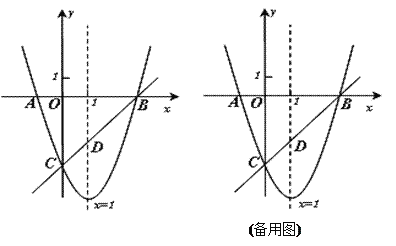
    【题目】如图，已知抛物线y=x2＋bx＋c与x轴交于A、B两点（A点在B点左侧），与y轴交于点C（0，－3），对称轴是直线x=1，直线BC与抛物线的对称轴交于点D．

    ⑴求抛物线的函数表达式；

    ⑵求直线BC的函数表达式；

    ⑶点E为y轴上一动点，CE的垂直平分线交CE于点F，交抛物线于P、Q两点，且点P在第三象限．①当线段PQ=AB时，求tan∠CED的值；②当以点C、D、E为顶点的三角形是直角三角形时，请直接写出点P的坐标．

    【答案】(1)y=x2－2x－3 (2) y=x－3 (3) P（，）（1－，－2），（1－，）

    【解析】

    已知了C点的坐标，即知道了OC的长，可在直角三角形BOC中根据∠BCO的正切值求出OB的长，即可得出B点的坐标．已知了△AOC和△BOC的面积比，由于两三角形的高相等，因此面积比就是AO与OB的比．由此可求出OA的长，也就求出了A点的坐标，然后根据A、B、C三点的坐标即可用待定系数法求出抛物线的解析式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

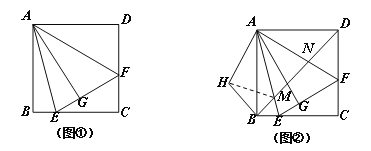
    【题目】如图①，在正方形ABCD中，△AEF的顶点E，F分别在BC，CD边上，高AG与正方形的边长相等，

    （1）求∠EAF的度数；

    （2）在图①中，连结BD分别交AE、AF于点M、N，将△ADN绕点A顺时针旋转90°至△ABH位置，连结MH，得到图②．求证：MN2＝MB2＋ ND2 ；

    （3）在图②中，若AG＝12， BM＝，直接写出MN的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）下面两个立体图形的名称是：__________，__________

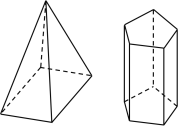
    （2）一个立体图形的三视图如下图所示，这个立体图形的名称是__________

    （3）画出下面立体图形的主视图．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

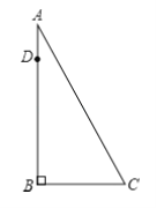
    【题目】如图，AB为一棵大树，在树上距地面10 米的D处有两只猴子，他们同时发现C处有一筐水果，一只猴子从D处往上爬到树顶A处，又沿滑绳AC滑到C处，另一只猴子从D滑到B，再由B跑到C处，已知两只猴子所经路程都为40米，求树高AB.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，AB∥CD，点P为定点，E、F分别是AB、CD上的动点．

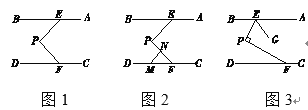
    (1)求证：∠P＝∠BEP＋∠PFD；

    (2)若点M为CD上一点，如图2，∠FMN＝∠BEP，且MN交PF于N.试说明∠EPF与∠PNM的数量关系，并证明你的结论；

    (3)移动E、F使得∠EPF＝90°，如图3，作∠PEG＝∠BEP，求∠AEG与∠PFD度数的比值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形纸片ABCD中，AB＝4，BC＝6，将△ABC沿AC折叠，使点B落在点E处，CE交AD于点F，则DF的长等于(　　)

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某草莓种植大户，今年从草莓上市到销售完需要20天，售价为15元/千克，成本y（元/千克）与第x天成一次函数关系，当x=10时，y=7，当x=15时，y=6.5．

    （1）求成本y（元/千克）与第x天的函数关系式并写出自变量x的取值范围；

    （2）求第几天每千克的利润w（元）最大？最大利润是多少？（利润=售价-成本）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在直角坐标系中，过原点O及点A（8，0），C（0，6）作矩形OABC、连结OB，点D为OB的中点，点E是线段AB上的动点，连结DE，作DF⊥DE，交OA于点F，连结EF．已知点E从A点出发，以每秒1个单位长度的速度在线段AB上移动，设移动时间为t秒．

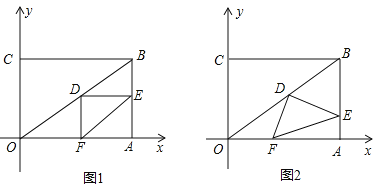
    （1）如图1，当t=3时，求DF的长．

    （2）如图2，当点E在线段AB上移动的过程中，∠DEF的大小是否发生变化？如果变化，请说明理由；如果不变，请求出tan∠DEF的值．

    （3）连结AD，当AD将△DEF分成的两部分的面积之比为1：2时，求相应的t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点，点.已知抛物线（是常数），顶点为.

    （Ⅰ）当抛物线经过点时，求顶点的坐标；

    （Ⅱ）若点在轴下方，当时，求抛物线的解析式；

    （Ⅲ） 无论取何值，该抛物线都经过定点.当时，求抛物线的解析式.

    查看答案和解析>>

    同步练习册答案