
【题目】若两个有理数的和等于这两个有理数的积,则称这两个有理数互为相依数.例如:有理数![]() 与3,因为
与3,因为![]() +3=
+3=![]() ×3.所以有理数与
×3.所以有理数与![]() 与3是互为相依数.
与3是互为相依数.
(1)直接判断下列两组有理数是否互为相依数,
①-5与-2;②-3与![]() ;
;
(2)若有理数![]() 与-7 互为相依数,求m的值;
与-7 互为相依数,求m的值;
(3)若有理数a与b互为相依数,b与c互为相反数,求式子5(ab+![]() c)-2(
c)-2(![]() a-b)-4的值;
a-b)-4的值;
(4)对于有理数a(a≠0,1),对它进行如下操作:取a的相依数,得到a1;取a1的倒数,得到a2;取a2的相依数,得到a3;取a3的倒数,得到a4;…,;依次按如上的操作得到一组数a1,a2,a3,…,an , 若a=![]() ,试着直接写出a1,a2,a3,…, a2018的和.
,试着直接写出a1,a2,a3,…, a2018的和.
【答案】(1)①-5与-2不互为相依数;②-3与![]() 互为相依数;(2)m=
互为相依数;(2)m=![]() ;(3)-4;(4)1013
;(3)-4;(4)1013![]()
【解析】
(1)根据互为相依数的定义进行判断即可;
(2)根据互为相依数的定义列方程:![]() +(-7)=
+(-7)=![]() ×(-7),解出即可;
×(-7),解出即可;
(3)去括号,合并同类项,并根据互为相依数和互为相反数的定义得:ab=a+b,b+c=0,代入可得结论;
(4)根据定义分别确定a1,a2,a3,…a2018,发现6个数一循环,用2018÷6得336余2,可得结论.
(1)①∵-5-2=-7,(-5)×(-2)=10,
∴-5-2≠(-5)×(-2),
∴-5与-2不是互为相依数;
②∵-3+![]() =-
=-![]() ,-3×
,-3×![]() =-
=-![]() ,
,
∴-3与![]() 是互为相依数;
是互为相依数;
(2)由题意得:![]() +(-7)=
+(-7)=![]() ×(-7),
×(-7),
解得:m=![]() ;
;
(3)∵有理数a与b互为相依数,
∴a+b=ab,
∵b与c互为相反数,
∴b+c=0,c=-b,
5(ab+![]() c)-2(
c)-2(![]() -b)-4,
-b)-4,
=5ab+7c-5a+2b-4,
=5(a+b)-7b-5a+2b-4,
=-4;
(4)当a=![]() 时,a1+
时,a1+![]() =
=![]() a1,a1=5,
a1,a1=5,
∵a1与a2互为倒数,
∴a2=![]() ,
,
则![]() +a3=
+a3=![]() a3,a3=-
a3,a3=-![]() ,
,
a4=-4,
-4+a5=-4a5,a5=![]() ,
,
a6=![]() ,
,
![]() +a7=
+a7=![]() a7,a7=5,
a7,a7=5,
∴6次一循环,
2018÷6=336…2,
∵a1+a2+a3+a4+a5+a6=5+![]() -
-![]() -4+
-4+![]() +
+![]() =3,
=3,
∴∴a1+a2+a3+a4+a5+a6+……+a2018
=336×3+a2017+a2018=336×3+a1+a2
=336×3+5+![]() =1013
=1013![]()


科目:初中数学 来源: 题型:
【题目】一辆汽车油箱现有汽油50L,如果不再加油,那么油箱中的油量![]() (L)随行驶里程
(L)随行驶里程![]() (km)的增加而减少,平均耗油量为0.11L/km.
(km)的增加而减少,平均耗油量为0.11L/km.
(1)写出表示![]() 与
与![]() 的函数关系式.
的函数关系式.
(2)指出自变量![]() 的取值范围.
的取值范围.
(3)汽车行驶200km时,油箱中还有多少汽油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一副三角板![]() 和
和![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
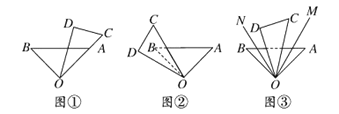
(1)如图①,点![]() ,
,![]() ,
,![]() 在一条直线上,
在一条直线上,![]() 的度数是______________.
的度数是______________.
(2)如图②,变化摆放位置将直角三角板![]() 绕点
绕点![]() 逆时针方向转动,若
逆时针方向转动,若![]() 恰好平分
恰好平分![]() ,则
,则![]() 的度数是__________;
的度数是__________;
(3)如图③,当三角板![]() 摆放在
摆放在![]() 内部时,作射线
内部时,作射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .如果三角板
.如果三角板![]() 在
在![]() 内绕点
内绕点![]() 任意转动,
任意转动,![]() 的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
的度数是否发生变化?如果不变,求其值;如果变化,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(1,-4) ,B(3,-3) ,C(1,-1).(每个小方格都是边长为一个单位长度的正方形)
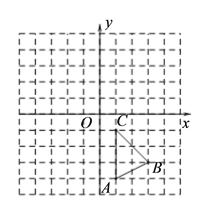
(1)将△ABC沿y轴方向向上平移5个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕点O顺时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点A旋转到点A2所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列各小题.
(1)先化简,再求值:![]() ,其中
,其中![]() 是最大的负整数,
是最大的负整数,![]() 是2的倒数;
是2的倒数;
(2)已知关于![]() 的方程
的方程![]() 与方程
与方程![]() 的解相同,求
的解相同,求![]() 的值;
的值;
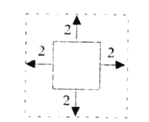
(3)用一根长为![]() (单位:
(单位:![]() )的铁丝,首尾相接围成一个正方形,要将它按如图所示的方式向外等距扩
)的铁丝,首尾相接围成一个正方形,要将它按如图所示的方式向外等距扩![]() ,得到新的正方形,求这根铁丝增加的长度.
,得到新的正方形,求这根铁丝增加的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场新进一批商品,每个成本价25元,销售一段时间发现销售量y(个)与销售单价x(元/个)之间成一次函数关系,如下表:

(1)求y与x之间的函数关系式;
(2)若该商品的销售单价在45元~80元之间浮动,
①销售单价定为多少元时,销售利润最大?此时销售量为多少?
②商场想要在这段时间内获得4550元的销售利润,销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台为了解本地区电视节目的收视情况,对部分市民开展了“你最喜爱的电视节目”的问卷调查(每人只填写一项),根据收集的数据绘制了两幅不完整的统计图(如图所示),根据要求回答下列问题:
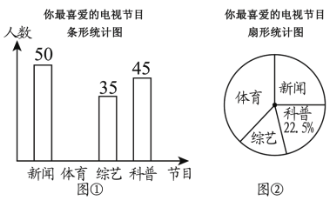
(1)本次问卷调查共调查了________名观众;图②中最喜爱“新闻节目”的人数占调查总人数的百分比为________;
(2)补全图①中的条形统计图;
(3)现有最喜爱“新闻节目”(记为![]() ),“体育节目”(记为
),“体育节目”(记为![]() ),“综艺节目”(记为
),“综艺节目”(记为![]() ),“科普节目”(记为
),“科普节目”(记为![]() )的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“
)的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“![]() ”和“
”和“![]() ”两位观众的概率.
”两位观众的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
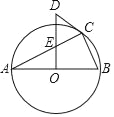
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,∠D=2∠A.
(1)求证:CD是⊙O的切线;
(2)求证:DE=DC;
(3)若OD=5,CD=3,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com