
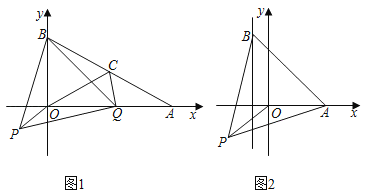
【题目】(1)问题发现:如图1,在平面直角坐标系中,A点的坐标为(2![]() ,0),点B的坐标为(0,2),连接AB,点C是AB的中点,点Q是线段AO上的动点,连接OC、CQ,以BQ为边构造等边△BPQ,连接OP、PQ.填空:
,0),点B的坐标为(0,2),连接AB,点C是AB的中点,点Q是线段AO上的动点,连接OC、CQ,以BQ为边构造等边△BPQ,连接OP、PQ.填空:
①OP与CQ的大小关系是 .
②OP的最小值为 .
(2)解决问题:在(1)的条件下,点Q运动的过程中当△ACQ为直角三角形时,求OP的长?
(3)拓展探究:如图2,当点B为直线x=﹣1上一动点,点A(2![]() ,0),连接AB,以AB为一边向下作等边△ABP,连接OP,请直接写出OP的最小值.
,0),连接AB,以AB为一边向下作等边△ABP,连接OP,请直接写出OP的最小值.
【答案】(1)①OP=CQ;②1;(2)OP的长为1或![]() ;(3)OP的最小值为
;(3)OP的最小值为![]() +1
+1
【解析】
(1)①证明△OBC是等边三角形,得出OB=BC,证明△PBO≌△QBC(SAS),可得出结论;
②当CQ⊥OA时,CQ值最小,得出最小值为![]() OB=1;
OB=1;
(2)分两种情况:①以Q点为直角顶点时,CQ⊥AO于点Q,②以C点为直角顶点时,CQ⊥AC,由直角三角形的性质可得出答案;
(3)以OA为对称轴,在x=﹣1上取D,E两点,作等边△ADE,连接EP,并延长EP交x轴于点F.证明△AEP≌△ADB(SAS),得出∠AEP=∠ADB=120°,可求出HF,OF,当OP⊥EF时,OP最小,则OP=![]() OF=
OF=![]() .
.
解:(1)问题发现
①∵A点的坐标为(2![]() ,0),点B的坐标为(0,2),
,0),点B的坐标为(0,2),
∴OA=2![]() ,OB=2,
,OB=2,
![]() ,
,
∴∠OBA=60°,
![]()
∵C是AB的中点,
![]()
∴OB=OC,
∴△OBC是等边三角形,
∴OB=BC,
∵△BPQ是等边三角形,
∴PB=BQ,∠PBQ=60°,
∴∠PBO=∠QBC,
∴△PBO≌△QBC(SAS),
∴OP=CQ,
②∵C是AB的中点,
∴CQ⊥OA时,CQ值最小,最小值为![]() OB=1,
OB=1,
∴OP的最小值为1.
故答案为:OP=CQ;1;
(2)解决问题
当三角形ACQ为直角三角形时,
①以Q点为直角顶点时,CQ⊥AO于点Q,
∵C为AB的中点,
∴AC=![]() ,
,
∴CQ=![]() AC=1,
AC=1,
即OP=1,
②以C点为直角顶点时,CQ⊥AC,
∵AC=2,
∴CQ=ACtan30°=2span>×![]() =
=![]() .
.
即OP=![]() .
.
综上所述:当三角形ACQ为直角三角形时,OP的长为1或![]() ;
;
(3)拓展探究
如图,以OA为对称轴,在x=﹣1上取D,E两点,作等边△ADE,连接EP,并延长EP交x轴于点F.
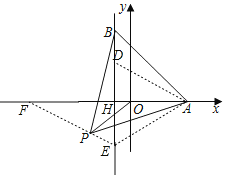
在△AEP与△ADB中,
∵AB=AP,∠BAD=∠PAE,AD=AE,
∴△AEP≌△ADB(SAS),
∴∠AEP=∠ADB=120°,
∴∠HEF=60°,且EH⊥AF,
∴HF=HA=![]() +1,
+1,
∴FO=FH+OH=![]() +2.
+2.
∴点P在直线EF上运动,
当OP⊥EF时,OP最小,
∴OP=![]() OF=
OF=![]() ,
,
则OP的最小值为![]() +1.
+1.


科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(3,0),点C的坐标为(0,4),OABC为矩形,反比例函数![]() 的图象过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.
的图象过AB的中点D,且和BC相交于点E,F为第一象限的点,AF=12,CF=13.
(1)求反比例函数![]() 和直线OE的函数解析式;
和直线OE的函数解析式;
(2)求四边形OAFC的面积?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家为了实现2020年全面脱贫目标,实施“精准扶贫”战略,采取异地搬迁,产业扶持等措施.使贫困户的生活条件得到改善,生活质量明显提高.某旗县为了全面了解贫困县对扶贫工作的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).
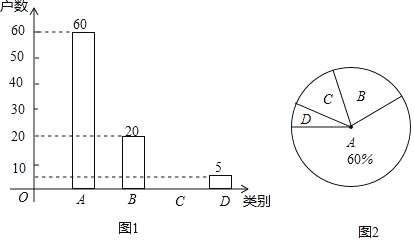
根据以上信息,解答下列问题:
(1)将图1补充完整;
(2)通过分析,贫困户对扶贫工作的满意度(A、B、C类视为满意)是 ;
(3)市扶贫办从该旗县甲乡镇3户、乙乡镇2户共5户贫困户中,随机抽取两户进行满意度回访,求这两户贫困户恰好都是同一乡镇的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了丰富学生课余生活,开展了“第二课堂”活动,推出了以下四种选修课程:![]() .绘画;
.绘画;![]() .唱歌;
.唱歌;![]() .跳舞;
.跳舞;![]() .演讲;
.演讲;![]() .书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.
.书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.
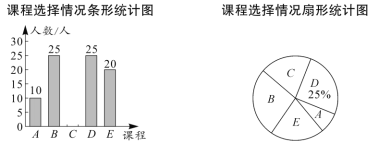
请结合统计图中的信息解决下列问题:
(1)这次抽查的学生人数是多少人?
(2)将条形统计图补充完整.
(3)求扇形统计图中课程![]() 所对应扇形的圆心角的度数.
所对应扇形的圆心角的度数.
(4)如果该校共有1200名学生,请你估计该校选择课程![]() 的学生约有多少人.
的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=4,若将△ABC绕点B顺时针旋转60°,点A的对应点为点A′,点C的对应点为点C′,点D为A′B的中点,连接AD.则点A的运动路径![]() 与线段AD、A′D围成的阴影部分面积是______.
与线段AD、A′D围成的阴影部分面积是______.
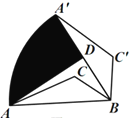
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
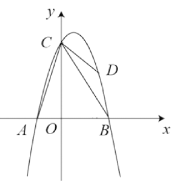
如图,抛物线![]() 经过点A(-2,0),B(4,0)两点,与
经过点A(-2,0),B(4,0)两点,与![]() 轴交于点C,点D是抛物线上一个动点,设点D的横坐标为
轴交于点C,点D是抛物线上一个动点,设点D的横坐标为![]() .连接AC,BC,DB,DC,
.连接AC,BC,DB,DC,
(1)求抛物线的函数表达式;
(2)△BCD的面积等于△AOC的面积的![]() 时,求
时,求![]() 的值;
的值;
(3)在(2)的条件下,若点M是![]() 轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两座建筑物的水平距离BC为40m,从D点测得A点的仰角为30°,B点的俯角为10°,求建筑物AB的高度(结果保留小数点后一位).
参考数据sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,![]() 取1.732.
取1.732.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在百货商场购进了A、B两种品牌的篮球,购买A品牌蓝球花费了2400元,购买B品牌蓝球花费了1950元,且购买A品牌蓝球数量是购买B品牌蓝球数量的2倍,已知购买一个B品牌蓝球比购买一个A品牌蓝球多花50元.
(1)求购买一个A品牌、一个B品牌的蓝球各需多少元?
(2)该学校决定再次购进A、B两种品牌蓝球共30个,恰逢百货商场对两种品牌蓝球的售价进行调整,A品牌蓝球售价比第一次购买时提高了10%,B品牌蓝球按第一次购买时售价的9折出售,如果这所中学此次购买A、B两种品牌蓝球的总费用不超过3200元,那么该学校此次最多可购买多少个B品牌蓝球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com