
【题目】某学校为了丰富学生课余生活,开展了“第二课堂”活动,推出了以下四种选修课程:![]() .绘画;
.绘画;![]() .唱歌;
.唱歌;![]() .跳舞;
.跳舞;![]() .演讲;
.演讲;![]() .书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.
.书法.学校规定:每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.
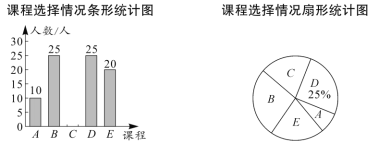
请结合统计图中的信息解决下列问题:
(1)这次抽查的学生人数是多少人?
(2)将条形统计图补充完整.
(3)求扇形统计图中课程![]() 所对应扇形的圆心角的度数.
所对应扇形的圆心角的度数.
(4)如果该校共有1200名学生,请你估计该校选择课程![]() 的学生约有多少人.
的学生约有多少人.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某公路隧道横截面为抛物线,其最大高度为6米,底部宽度OM为12米. 现以O点为原点,OM所在直线为x轴建立直角坐标系.

(1)直接写出点M及抛物线顶点P的坐标;
(2)求这条抛物线的解析式;
(3)若要搭建一个矩形“支撑架”AD- DC- CB,使C、D点在抛物线上,A、B点在地面OM上,则这个“支撑架”总长的最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旋转变换是解决数学问题中一种重要的思想方法,通过旋转变换可以将分散的条件集中到一起,从而方便解决问题.
已知,△ABC中,AB=AC,∠BAC=α,点D、E在边BC上,且∠DAE=![]() α.
α.
(1)如图1,当α=60°时,将△AEC绕点A顺时针旋转60°到△AFB的位置,连接DF,
①求∠DAF的度数;
②求证:△ADE≌△ADF;
(2)如图2,当α=90°时,猜想BD、DE、CE的数量关系,并说明理由;
(3)如图3,当α=120°,BD=4,CE=5时,请直接写出DE的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
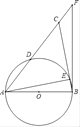
【题目】如图,在等腰△ABC中,AB=BC,以AB为直径的半圆分别交AC、BC于点D、E两点,BF与⊙O相切于点B,交AC的延长线于点F.
(1)求证:D是AC的中点;
(2)若AB=12,sin∠CAE=![]() ,求CF的值.
,求CF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
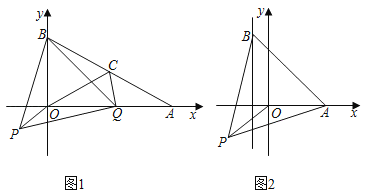
【题目】(1)问题发现:如图1,在平面直角坐标系中,A点的坐标为(2![]() ,0),点B的坐标为(0,2),连接AB,点C是AB的中点,点Q是线段AO上的动点,连接OC、CQ,以BQ为边构造等边△BPQ,连接OP、PQ.填空:
,0),点B的坐标为(0,2),连接AB,点C是AB的中点,点Q是线段AO上的动点,连接OC、CQ,以BQ为边构造等边△BPQ,连接OP、PQ.填空:
①OP与CQ的大小关系是 .
②OP的最小值为 .
(2)解决问题:在(1)的条件下,点Q运动的过程中当△ACQ为直角三角形时,求OP的长?
(3)拓展探究:如图2,当点B为直线x=﹣1上一动点,点A(2![]() ,0),连接AB,以AB为一边向下作等边△ABP,连接OP,请直接写出OP的最小值.
,0),连接AB,以AB为一边向下作等边△ABP,连接OP,请直接写出OP的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数y=![]() (a>0,a为常数)和y=
(a>0,a为常数)和y=![]() 在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y=![]() 的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y=![]() 的图象于点A;MD⊥y轴于点D,交y=
的图象于点A;MD⊥y轴于点D,交y=![]() 的图象于点B,当点M在y=
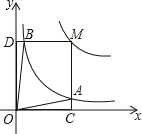
的图象于点B,当点M在y=![]() 的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论是( )
的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论是( )
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:在平面直角坐标系中,若两点P、Q的坐标分别是P(x1,y1)、
Q(x2,y2),则P、Q这两点间的距离为|PQ|=![]() .如P(1,2),Q(3,4),则|PQ|=
.如P(1,2),Q(3,4),则|PQ|=![]() =2
=2![]() .
.
对于某种几何图形给出如下定义:符合一定条件的动点形成的图形,叫做符合这个条件的点的轨迹.如平面内到线段两个端点距离相等的点的轨迹是这条线段的垂直平分线.
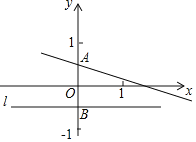
解决问题:如图,已知在平面直角坐标系xOy中,直线y=kx+![]() 交y轴于点A,点A关于x轴的对称点为点B,过点B作直线l平行于x轴.
交y轴于点A,点A关于x轴的对称点为点B,过点B作直线l平行于x轴.
(1)到点A的距离等于线段AB长度的点的轨迹是 ;
(2)若动点C(x,y)满足到直线l的距离等于线段CA的长度,求动点C轨迹的函数表达式;
问题拓展:(3)若(2)中的动点C的轨迹与直线y=kx+![]() 交于E、F两点,分别过E、F作直线l的垂线,垂足分别是M、N,求证:①EF是△AMN外接圆的切线;②
交于E、F两点,分别过E、F作直线l的垂线,垂足分别是M、N,求证:①EF是△AMN外接圆的切线;②![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com