
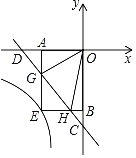
【题目】如图,在平面直角坐标系xOy中,直线y=﹣x﹣2与x轴,y轴分别交于点D,C.点G,H是线段CD上的两个动点,且∠GOH=45°,过点G作GA⊥x轴于A,过点H作HB⊥y轴于B,延长AG,BH交于点E,则过点E的反比例函数y=![]() 的解析式为_____.
的解析式为_____.
【答案】y=![]()
【解析】
过点G作GP⊥GO,交OH的延长线于点P,过点P作PN⊥AE,交AE延长线于N,设点A(-![]() ,0)则AO=
,0)则AO=![]() ,DO=2,AD=2-
,DO=2,AD=2-![]() ,由“AAS”可证△GAO≌△PNG,可得NP=AG=2-
,由“AAS”可证△GAO≌△PNG,可得NP=AG=2-![]() ,AO=GN=
,AO=GN=![]() ,可求点P坐标,求出一次函数解析式,可求点H的纵坐标,即可求解.
,可求点P坐标,求出一次函数解析式,可求点H的纵坐标,即可求解.
解:如图,过点G作GP⊥GO,交OH的延长线于点P,过点P作PN⊥AE,交AE延长线于N,
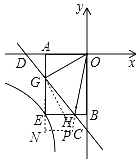
设点A(-![]() ,0)
,0)
∴AO=![]() ,
,
∵直线y=﹣x﹣2与x轴,y轴分别交于点D,C,
∴点D(﹣2,0),∠ADC=45°,
∴DO=2,AD=2﹣![]() ,
,
∵AE⊥OD,
∴∠ADG=∠AGD=45°,
∴AD=AG=2﹣![]() ,
,
∵GP⊥GO,∠GOH=45°,
∴∠GPO=∠GOP=45°,
∴GP=GO,
∵∠AGO+∠AOG=90°,∠AGO+∠NGP=90°,
∴∠AOG=∠NGP,
又∵∠GNP=∠GAO=90°,GO=GP,
∴△GAO≌△PNG(AAS),
∴NP=AG=2﹣![]() ,AO=GN=
,AO=GN=![]() ,
,
∴AN=2,
∴点P(2﹣2![]() ,﹣2),
,﹣2),
∴直线OP解析式为:y=![]() x,
x,
联立方程组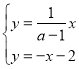
∴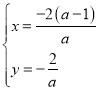
∴点H的纵坐标为![]() ,
,
∴点E(![]() ,
,![]() )
)
∵反比例函数y=![]() 的图象过点E,
的图象过点E,
∴k=![]() ×(
×(![]() )=2,
)=2,
∴反比例函数解析式为:y=![]() ,
,
故答案为:y=![]() .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为10,点E,F分别为BC,AB边的中点.连接AE、DF,两线交于点H,连接BH并延长,交边AD于点G.下列结论:①△ABE≌△DAF,②cos∠BAE=![]() ,③
,③![]() :S四边形CDHE=1:11,④AG=
:S四边形CDHE=1:11,④AG=![]() 其中正确的是( )
其中正确的是( )
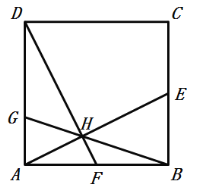
A.①③④B.①②③
C.①④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:在平面直角坐标系中,若两点P、Q的坐标分别是P(x1,y1)、
Q(x2,y2),则P、Q这两点间的距离为|PQ|=![]() .如P(1,2),Q(3,4),则|PQ|=
.如P(1,2),Q(3,4),则|PQ|=![]() =2
=2![]() .
.
对于某种几何图形给出如下定义:符合一定条件的动点形成的图形,叫做符合这个条件的点的轨迹.如平面内到线段两个端点距离相等的点的轨迹是这条线段的垂直平分线.
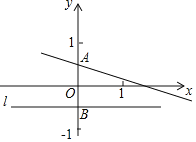
解决问题:如图,已知在平面直角坐标系xOy中,直线y=kx+![]() 交y轴于点A,点A关于x轴的对称点为点B,过点B作直线l平行于x轴.
交y轴于点A,点A关于x轴的对称点为点B,过点B作直线l平行于x轴.
(1)到点A的距离等于线段AB长度的点的轨迹是 ;
(2)若动点C(x,y)满足到直线l的距离等于线段CA的长度,求动点C轨迹的函数表达式;
问题拓展:(3)若(2)中的动点C的轨迹与直线y=kx+![]() 交于E、F两点,分别过E、F作直线l的垂线,垂足分别是M、N,求证:①EF是△AMN外接圆的切线;②
交于E、F两点,分别过E、F作直线l的垂线,垂足分别是M、N,求证:①EF是△AMN外接圆的切线;②![]() 为定值.
为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都市为了扎实推进精准扶贫工作,出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为A,B,C,D类贫困户,为检查帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成如图两幅不完整的统计图.请根据图中信息,回答下列问题:
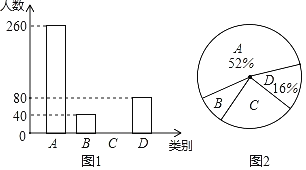
(1)本次抽样调查了多少户贫困户?
(2)成都市共有9100户贫困户,请估计至少得到4种帮扶措施的大约有多少户?
(3)2020年是精准扶贫攻关年,为更好地做好工作,现准备从D类贫困户中的甲、乙、丙、丁四户中随机选取两户进行试点帮扶,请用树状图或列表法求出恰好选中乙和丙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在四边形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O交边DC于E、F两点,AD=1,BC=5,设⊙O的半径长为r.
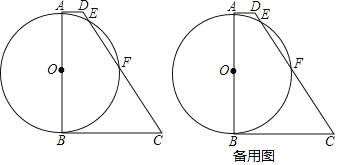
(1)联结OF,当OF∥BC时,求⊙O的半径长;
(2)过点O作OH⊥EF,垂足为点H,设OH=y,试用r的代数式表示y;
(3)设点G为DC的中点,联结OG、OD,△ODG是否能成为等腰三角形?如果能,试求出r的值;如不能,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
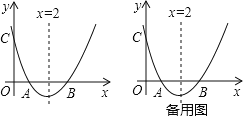
(1)求抛物线的函数表达式;
(2)设D为抛物线的顶点,连接DA、DB,试判断△ABD的形状,并说明理由;
(3)设P为对称轴上一动点,要使PC﹣PB的值最大,求出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-2![]() x+m=0有两个不相等的实数根.
x+m=0有两个不相等的实数根.
(1)求实数m的最大整数值;
(2)在(1)的条件下,方程的实数根是![]() 、
、![]() ,求代数式
,求代数式![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com