
【题目】如图,正方形ABCD的边长为10,点E,F分别为BC,AB边的中点.连接AE、DF,两线交于点H,连接BH并延长,交边AD于点G.下列结论:①△ABE≌△DAF,②cos∠BAE=![]() ,③
,③![]() :S四边形CDHE=1:11,④AG=
:S四边形CDHE=1:11,④AG=![]() 其中正确的是( )
其中正确的是( )
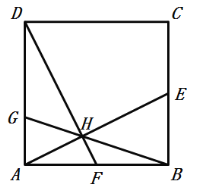
A.①③④B.①②③
C.①④D.②③④
【答案】A
【解析】
利用两对应边成比例且夹角相等可证得①正确;先求得![]() 的长,根据角的余弦函数即可说明②错误;分别求得
的长,根据角的余弦函数即可说明②错误;分别求得![]() 、
、![]() 以及
以及![]() 的面积,即可证得③正确;作HQ⊥AB于Q,利用相似三角形的性质求得
的面积,即可证得③正确;作HQ⊥AB于Q,利用相似三角形的性质求得![]() 、
、![]() 、
、![]() 的长,再利用平行线的性质求得
的长,再利用平行线的性质求得![]() 的长,④正确;即可判断.
的长,④正确;即可判断.
∵正方形ABCD的边长为10,点E,F分别为BC,AB边的中点,
∴![]() ,
,![]() ,
,
∴![]() ,∠ABE=∠DAF=90
,∠ABE=∠DAF=90![]() ,
,
∴△ABE≌△DAF,故①正确;
在△ABE中,∠ABE=90![]() ,
,
∴![]() ,
,
∴cos∠BAE=![]() ,故②错误;
,故②错误;
![]() ,
,
∵△ABE≌△DAF,
∴∠AFH=∠AEB,
∴△AFH![]() △AEB,
△AEB,
∴ ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]() ,
,
∴![]() ,故③正确;
,故③正确;
∵△AFH![]() △AEB,
△AEB,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
作HQ⊥AB于Q,
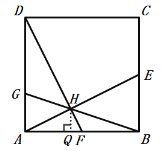
∴HQ∥BE,
∴△AHQ![]() △AEB,
△AEB,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵HQ∥AG,
∴![]() ,即
,即![]() ,
,
∴![]() ,故④正确;
,故④正确;
综上,①③④正确,
故选:A.


科目:初中数学 来源: 题型:
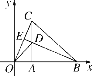
【题目】如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=![]() ,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是________.
,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,O点在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线,与AB的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)若AB=3,AC=4,求线段PB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是4cm
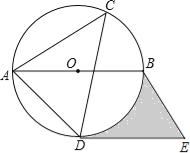
(1)请判断DE与⊙O的位置关系,并说明理由;
(2)求图中阴影部分的面积(结果用π表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.
(1)求证:PB是⊙O的切线;
(2)若OC=3,AC=4,求sinE的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
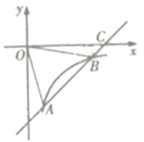
【题目】如图,已知一次函数y= kx +b的图象交反比例函数![]() 的图象于点A(2,-4)和点B(h,-2),交x轴于点C.
的图象于点A(2,-4)和点B(h,-2),交x轴于点C.
(1)求这两个函数的解析式;
(2)连接QA、OB.求△AOB的面积;
(3)请直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
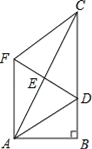
【题目】如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
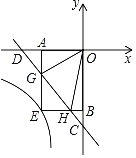
【题目】如图,在平面直角坐标系xOy中,直线y=﹣x﹣2与x轴,y轴分别交于点D,C.点G,H是线段CD上的两个动点,且∠GOH=45°,过点G作GA⊥x轴于A,过点H作HB⊥y轴于B,延长AG,BH交于点E,则过点E的反比例函数y=![]() 的解析式为_____.
的解析式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
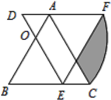
【题目】△ABC为等边三角形,点O为AB边上一点,且BO=2AO=4,将△ABC绕点O逆时针旋转60°得△DEF,则图中阴影部分的面积为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com