
【题目】如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.
(1)求证:PB是⊙O的切线;
(2)若OC=3,AC=4,求sinE的值.

【答案】(1)证明见解析;(2)![]()
【解析】
(1)要证明是圆的切线,须证明过切点的半径垂直,所以连接OB,证明OB⊥PE即可.
(2)要求sinE,首先应找出∠E所在的直角三角形,然后利用直角三角函数求解即可.而sinE既可放在直角三角形EAP中,也可放在直角三角形EBO中,所以利用相似三角形的性质求出EP或EO的长即可解决问题
(1)证明:连接OB
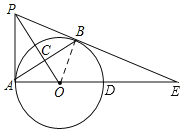
∵PO⊥AB,
∴AC=BC,
∴PA=PB,
在△PAO和△PBO中
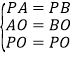 ,
,
∴△PAO和≌△PBO,
∴∠OBP=∠OAP=90°,
∴PB是⊙O的切线.
(2)连接BD,则BD∥PO,且BD=2OC=6
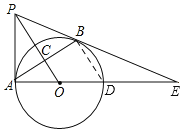
在Rt△ACO中,OC=3,AC=4
∴AO=5
在Rt△ACO与Rt△PAO中,
∠APO=∠APO,
∠PAO=∠ACO=90°
∴△ACO△PAO
∴![]()
∴PO=![]() ,PA=
,PA=![]()
∴PB=PA=![]()
在△EPO与△EBD中,
BD∥PO
∴△EPO∽△EBD
∴![]() ,
,
解得EB=![]() ,PE=
,PE=![]() ,
,
∴sinE=![]() .
.


科目:初中数学 来源: 题型:
【题目】某超市在“元旦”期间对顾客实行优惠,规定一次性购物优惠办法:
少于200元,不予优惠;高于200元但低于500元时,九折优惠;消费500元或超过500元时,其中500元部分给予九折优惠,超过500元部分给予八折优惠.根据优惠条件完成下列任务:
(1)王老师一次性购物600元,他实际付款多少元?
(2)若顾客在该超市一次性购物x元,当x小于500但不小于200时,他实际付款0.9x,当x大于或等于500元时,他实际付款多少元?(用含x的代数式表示)
(3)如果王老师两次购物货款合计820元,第一次购物的货款为a元(200<a<300),用含a的式子表示王老师两次购物实际付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上(不与A、O重合)的一个动点,过点P作PE⊥PB且PE交边CD于点E.
(1)求证:PB=PE;
(2)过点E作EF⊥AC于点F,如图2.若正方形ABCD的边长为2,则在点P运动的过程中,PF的长度是否发生变化?若不变,请直接写出这个不变的值;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级甲、乙两班分别选5名同学参加“学雷锋见行动”演讲比赛,其预赛成绩如图:
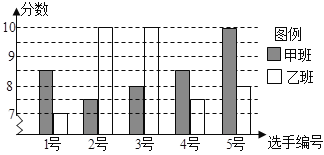
(1)根据上图求出下表中的a,b,c的值(单位:分);
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | a | 8.5 | 0.7 |
乙班 | b | 8 | c | 1.6 |
(2)学校决定在甲、乙两班中选取预赛成绩较好的5人参加该活动的县级演讲比赛,求这5人预赛成绩的平均分数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先尺规作图,后进行计算:如图,△ABC中,∠A=105°.
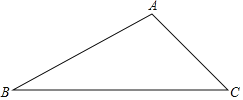
(1)试求作一点P,使得点P到B、C两点的距离相等,并且到∠ABC两边的距离相等(尺规作图,不写作法,保留作图痕迹).
(2)在(1)的条件下,若∠ACP=30°,则∠PBC的度数为 °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠AOB=90°,OC平分∠AOB,点P在射线OC上.点E在射线OA上,点F在射线OB上,且∠EPF=90°.
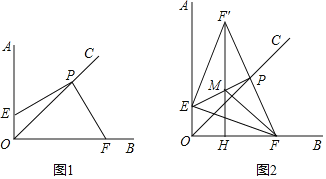
(1)如图1,求证:PE=PF;
(2)如图2,作点F关于直线EP的对称点F′,过F′点作FH⊥OF于H,连接EF′,F′H与EP交于点M.连接FM,图中与∠EFM相等的角共有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题:
(1)线段CD表示轿车在途中停留了 h;
(2)求线段DE对应的函数解析式;
(3)求轿车从甲地出发后经过多长时间追上货车.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD(纸片)折叠,使点B与AD边上的点K重合,EG为折痕;点C与AD边上的点K重合,FH为折痕.已知∠1=67.5°,∠2=75°,EF=![]() +1,求BC的长.
+1,求BC的长.
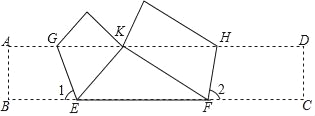
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com